Сначала докажем, что если окружность описана около прямоугольного треугольника, то ее центр лежит на гипотенузе. пусть, дан треугольник АВС с прямым углом С пусть, точка О-центр описанной окружности. рассмотрим следующие треугольники: ВОС-равнобедренный, ∠ОВС=∠ОСВ, АОС-равнобедренный, ∠ОАС=∠ОСА но сумма углов ВСО и АСО=90°, значит, сумма углов САО + СВО=ВСО +АСО=90° Сумма углов выпуклого четырехугольника =360°,значит, АОВ=360-90-90=180°, то есть развернутый угол Кроме того, ОВ=ОА, поскольку О-центр окружности
задача1 АС = 12 см, ВС = 5 см; АВ=√(СВ²+АС²)=√(144+25)=13 см ОА=ОВ=13:2=7,5 см.
задача2. АС = 16 см, ∠В = 30°. АВ=16:sin30°=16:0,5=32 ОА=ОВ=32:2=16 см
Назовём данный треугольник АВС.
ВВ1- высота к АС.
АА1=СС1 - высоты к равным боковым сторонам.
Высота равнобедренного треугольника, проведенная к основанию, является его биссектрисой и медианой. ⇒
АВ1=СВ1=30:2=15 см
∆ АВВ1=∆ СВВ1 ( по трем сторонам).
Из ∆ АВВ1 по т.Пифагора
ВВ1=√(AB²-AB1²)=√(17²-15²)=8 см
Высоты к боковым сторонам найдем из площади ∆ АВС
Заметим, что ∆ АВС - тупоугольный ( АС² > АВ²+ВС²), поэтому высоты, проведенные к боковым сторонам тупоугольного треугольника, лежат вне его.
S(ABC)=BB1•AC:2=8•15=120 см²
AA1=2S(ABC):BC
AA1=CC1=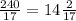 см
см
пусть, дан треугольник АВС с прямым углом С
пусть, точка О-центр описанной окружности.
рассмотрим следующие треугольники:
ВОС-равнобедренный, ∠ОВС=∠ОСВ,
АОС-равнобедренный, ∠ОАС=∠ОСА
но сумма углов ВСО и АСО=90°, значит,
сумма углов САО + СВО=ВСО +АСО=90°
Сумма углов выпуклого четырехугольника =360°,значит, АОВ=360-90-90=180°, то есть развернутый угол
Кроме того, ОВ=ОА, поскольку О-центр окружности
задача1
АС = 12 см, ВС = 5 см;
АВ=√(СВ²+АС²)=√(144+25)=13 см
ОА=ОВ=13:2=7,5 см.
задача2.
АС = 16 см, ∠В = 30°.
АВ=16:sin30°=16:0,5=32
ОА=ОВ=32:2=16 см