BN ∩ AD = L
ΔBNC = ΔLND по стороне и двум углам прилежащим к ней (CN=DN по условию; ∠BNC=∠LND как вертикальные; ∠NCB=∠NDL как накрест лежащие), поэтому BC=LD.
Пусть BM = x, тогда BC = 2x.
LD=BC=AD ⇒ AL=2BC=4x
ΔMOB ~ ΔAOL по трём углам (∠MOB=∠AOL как вертикальные; ∠OBM=∠OLA и ∠OMB=∠OAL как накрест лежащие), поэтому
ответ: 1/4.
BN ∩ AD = L
ΔBNC = ΔLND по стороне и двум углам прилежащим к ней (CN=DN по условию; ∠BNC=∠LND как вертикальные; ∠NCB=∠NDL как накрест лежащие), поэтому BC=LD.
Пусть BM = x, тогда BC = 2x.
LD=BC=AD ⇒ AL=2BC=4x
ΔMOB ~ ΔAOL по трём углам (∠MOB=∠AOL как вертикальные; ∠OBM=∠OLA и ∠OMB=∠OAL как накрест лежащие), поэтому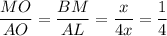
ответ: 1/4.