Точки М, що лежать поза колом, проведено до кола дві дотичні МА і МБ; B де А i В - точки дотику, Z MBA% 3D 60 °. Знайдіть відстань від точки М до центральної машини, якщо радіус кола дорівнює 10 см 10 см 15 см 20 см 25 см До іть будь ласка!!))
судя по тому, что ∠авс= 120°, параллелепипед не прямоугольный, а прямой. это "две большие разницы".
итак, высота параллелепипеда равна 9см, а в основании прямого параллелепипеда лежит параллелограмм со стороной вс = 5 см, диагональю ас=7см и углом авс = 120°. по теореме косинусов попробуем найти сторону ав.
ответ:
v = 5√3/6 ед³.
sбок = 144 ед².
объяснение:
судя по тому, что ∠авс= 120°, параллелепипед не прямоугольный, а прямой. это "две большие разницы".
итак, высота параллелепипеда равна 9см, а в основании прямого параллелепипеда лежит параллелограмм со стороной вс = 5 см, диагональю ас=7см и углом авс = 120°. по теореме косинусов попробуем найти сторону ав.
ас² =ав²+вс² - 2·ав·вс·cos120. cos120 = -cos60 = - 1/2.
49 = ab²+25 - 2·ab·5·(-1/2) =>
ав²+5·ав -24 =0 => ab = 3cм
so = ab·bc·sin120 = 3·5·√3/2.
v = so·h = (3·5·√3/2)·9 = 5√3/6 ед³. (площадь основания, умноженная на высоту).
sбок = р·h = 2(3+5)·9 = 144 ед² ( периметр, умноженный на высоту)
Объяснение:
Дано: Окр.О,R;
MO = L
MB₁, MB₂, A₂A₁ - касательные.
Найти: Р (ΔА₁МА₂)
1. Рассмотрим ΔОМВ₁.
Радиус, проведенный в точку касания, перпендикулярен касательной.⇒ ОВ₁ ⊥ МВ₁ ⇒ ΔОМВ₁ - прямоугольный.
По теореме Пифагора найдем МВ₁ :
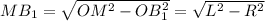
2. Отрезки касательных к окружности, проведённые из одной точки, равны.⇒ МВ₁ = МВ₂ =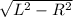
3. Рассмотрим ΔА₁МА₂
Р (ΔА₁МА₂) = А₂М + МА₁ + А₁А₂
А₁А₂ = А₁С + СА₂
А₂С = А₂В₂ ; СА₁ = А₁В₁ (отрезки касательных)
Тогда:
Р (ΔА₁МА₂) = А₂М + МА₁ + А₁С + СА₂ = А₂М + МА₁ + А₁В₁ + А₂В₂
А₂М + А₂В₂ = МВ₂
МА₁ + А₁В₁ = МВ₁
⇒ Р (ΔА₁МА₂) = МВ₂ + МВ₁ =