Координаты точки на оси Ox : A (6;0)
Координаты точки на оси Oy : B (0;10)
Так как 6<10, значит, центр окружности лежит слева от оси Oy.
Координаты центра окружности на оси Ox : С(-m;0)
R = CA = m + 6
ΔBOC , R = CB, теорема Пифагора :
R² = m² + 10²
(m + 6)² = m² + 10²
m² + 12m + 36 = m² + 100
12m = 64;
Общее уравнение окружности с центром в точке С и радиусом R
Так как абсцисса центра окружности отрицательная, то в первой скобке должен быть знак плюс.
Если подгонять ответ под схему в условии, то знак минус придётся убрать в числитель дроби :
Уравнение окружности с центром в точке (х0;у0) радиуса r имеет вид
(х-х0)^2+(у-у0)^2=r^2.
По условию задачи центр окружности находится на оси Ох, а значит (х0;у0)=(х0;0) и уравнение окружности примет вид
(х-х0)^2+у^2=r^2.
Найдем х0 и r.
По условию окружность проходит через точки (6;0) и (0;10), а значит координаты этих точек удовлетворяют уравнению окружности, т.е.
{(6-х0)^2=r^2; (x0)^2+100=r^2}
Правые части последних выражений равны, а значит равны и левые части:
(6-х0)^2=(х0)^2+100
36-12х0+(х0)^2-(х0)^2=100
-12х0=64
х0=-64/12=-16/3.
Найдем r^2:
(-16/3)^2+100=r^2
(256/9)+100=r^2
1156/9=r^2
r^2=(34/3)^2.
Подставляя, найденные значения х0 и r в уравнение окружности, получим искомое уравнение окружности:
(х+(16/3))^2+у^2=(34/3)^2
Координаты точки на оси Ox : A (6;0)
Координаты точки на оси Oy : B (0;10)
Так как 6<10, значит, центр окружности лежит слева от оси Oy.
Координаты центра окружности на оси Ox : С(-m;0)
R = CA = m + 6
ΔBOC , R = CB, теорема Пифагора :
R² = m² + 10²
(m + 6)² = m² + 10²
m² + 12m + 36 = m² + 100
12m = 64;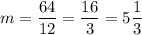
Общее уравнение окружности с центром в точке С и радиусом R
Так как абсцисса центра окружности отрицательная, то в первой скобке должен быть знак плюс.
Если подгонять ответ под схему в условии, то знак минус придётся убрать в числитель дроби :
Уравнение окружности с центром в точке (х0;у0) радиуса r имеет вид
(х-х0)^2+(у-у0)^2=r^2.
По условию задачи центр окружности находится на оси Ох, а значит (х0;у0)=(х0;0) и уравнение окружности примет вид
(х-х0)^2+у^2=r^2.
Найдем х0 и r.
По условию окружность проходит через точки (6;0) и (0;10), а значит координаты этих точек удовлетворяют уравнению окружности, т.е.
{(6-х0)^2=r^2; (x0)^2+100=r^2}
Правые части последних выражений равны, а значит равны и левые части:
(6-х0)^2=(х0)^2+100
36-12х0+(х0)^2-(х0)^2=100
-12х0=64
х0=-64/12=-16/3.
Найдем r^2:
(-16/3)^2+100=r^2
(256/9)+100=r^2
1156/9=r^2
r^2=(34/3)^2.
Подставляя, найденные значения х0 и r в уравнение окружности, получим искомое уравнение окружности:
(х+(16/3))^2+у^2=(34/3)^2