Трегольники ao1o2 и abc,а также треугольнки abc и ao3o4 подобны по 3 признаку и имеют одинаковые коэффициенты подобия.найдите стороны треугольника abc. с решением ,
а)Даны стороны треугольника АВ и АС и угол между ними.
На произвольной прямой отложим отрезок, равный длине стороны АС, отметим на нём точки А и С.
Из вершины А заданного угла проведем полуокружность произвольного радиуса и сделаем насечки М и К на его сторонах. АМ=АК= радиусу проведенной окружности.
Из т.А на отложенном отрезке тем же раствором циркуля проведем полуокружность. Точку пересечения с АС обозначим К1.
От К1 циркулем проведем полуокружность радиусом, равным длине отрезка КМ, соединяющим стороны заданного угла.
Эта полуокружность пересечется с первой. Через точку пересечения проведем от т. А луч и отложим на нем отрезок, равный данной стороне АВ, отметим точку В. . Соединим В и С.
Искомый треугольник построен.
б) Биссектриса проводится так же, как проводится срединный перпендикуляр к отрезку.
Из точек, взятых на сторонах угла на равном расстоянии от его вершины А ( отмеряем циркулем) проводим полуокружности равного радиуса так, чтобы они пересеклись. Через точки их пересечения и А проводим луч. Треугольник АМ1К! - равнобедренный по построению, АЕ - перпендикулярен М1К1 и делит его пополам.
Треугольники АЕМ1 и АЕК1 равны по гипотенузе и общему катету. Поэтому их углы при А равны. АЕ - биссектриса.
∠А=180°-(90°+60°)=180°-150°=30°-по теореме о сумме углов в треугольнике.
В условии сказано что сумма гипотенузы и меньшего катета равна 30 см. Чтобы понять какой катет меньший, для это нужно посмотреть на углы, которые находятся напротив катетов. Напротив ∠А находится самый маленький катет, т.к ∠А самый маленький в этом треугольнике.
Значит, СВ+АВ=30 см.
Напротив угла равного 30° лежит катет СВ⇒ он равен половине гипотенузы АВ.
а)Даны стороны треугольника АВ и АС и угол между ними.
На произвольной прямой отложим отрезок, равный длине стороны АС, отметим на нём точки А и С.
Из вершины А заданного угла проведем полуокружность произвольного радиуса и сделаем насечки М и К на его сторонах. АМ=АК= радиусу проведенной окружности.
Из т.А на отложенном отрезке тем же раствором циркуля проведем полуокружность. Точку пересечения с АС обозначим К1.
От К1 циркулем проведем полуокружность радиусом, равным длине отрезка КМ, соединяющим стороны заданного угла.
Эта полуокружность пересечется с первой. Через точку пересечения проведем от т. А луч и отложим на нем отрезок, равный данной стороне АВ, отметим точку В. . Соединим В и С.
Искомый треугольник построен.
б) Биссектриса проводится так же, как проводится срединный перпендикуляр к отрезку.
Из точек, взятых на сторонах угла на равном расстоянии от его вершины А ( отмеряем циркулем) проводим полуокружности равного радиуса так, чтобы они пересеклись. Через точки их пересечения и А проводим луч. Треугольник АМ1К! - равнобедренный по построению, АЕ - перпендикулярен М1К1 и делит его пополам.
Треугольники АЕМ1 и АЕК1 равны по гипотенузе и общему катету. Поэтому их углы при А равны. АЕ - биссектриса.
10 см.
Объяснение:
✓РЕШЕНО МУДROST✓
Если ∠С = 90°, а ∠В=60°, то
∠А=180°-(90°+60°)=180°-150°=30°-по теореме о сумме углов в треугольнике.
В условии сказано что сумма гипотенузы и меньшего катета равна 30 см. Чтобы понять какой катет меньший, для это нужно посмотреть на углы, которые находятся напротив катетов. Напротив ∠А находится самый маленький катет, т.к ∠А самый маленький в этом треугольнике.
Значит, СВ+АВ=30 см.
Напротив угла равного 30° лежит катет СВ⇒ он равен половине гипотенузы АВ.
Пусть х см - гипотенуза АВ, то
СВ=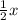
Составим и решим уравнение:
x+0,5х=30
1,5х=30
х=30:1,5
х=20
Итак: гипотенуза АВ=20 см, тогда
СВ=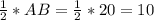 см.
см.
✓РЕШЕНО МУДROST✓