Треугольник ABC - фигура, полученная в результате поворота треугольника АВС вокруг начала координат на угол α против часовой стрелки.
а) Выполните построения отображений вершин треугольника АВС при данном повороте.
б) Найдите градусную меру угла поворота α.
Сторона квадрата равна а. В данный квадрат вписан квадрат таким образом, что его вершины делят сторону данного квадрата в отношении 5:6. Найди площадь вписанного квадрата.
Объяснение:
Тк каждая сторона бОльшего квадрата разделена в отношении 5:6 , то все прямоугольные треугольники равны по 3-м катетам. И значит их площади равны.
S(вписанного квадрата )= S(большего квадрата )-4*S( белых треуг.).
Всего частей на сторону большего квадрата приходится 5+6=11 , поэтому меньший катет равен 5/11*а , больший катет равен 6/11*а.
Тогда площадь каждого белого треугольника
S=1/2* 5/11*а * 6/11*а=(15/121)*a² (ед²).
S(вписанного ЧЕРНОГО кв. )=а²- 4*(15/121)*а²=а²(1-60/121)=61/121*а².
orjabinina
Вершины треугольника А(2;0) , В(5;3) , С(3;7). Найдите уравнение прямой, проходящей через вершину В и параллельной медиане АМ треугольника
Объяснение:
Пусть прямая , проходящая через точку В будет m. Тк m ║ AM, то у прямых одинаковое к.
1) Ищем уравнение прямой АМ.
Первая точка А(2;0), вторая М(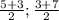
) или М(4;5) : 
⇒
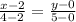5(x-2)=2y или у=2,5х-5 ⇒ к(АМ)=2,5 и тогда к(m)=2,5.
2)Прямой у=кх+b принадлежит точка В(5;3) и к=2,5 :
3=2,5*5+b ⇒ b=-9,5. Получили у=2,5х-9,5
=================
Формула для вычисления координат середины отрезка х=(х₁+х₂):2 ,
у=(у₁+у₂):2 где (х₁;у₁), (х₂;у₂) координаты концов отрезка , (х;у )-координаты середины.
Если прямая проходит через точки М1(х1; у1) и М2(х2; y2) то уравнение прямой (x - x1)/(x2 - x1) = (y - y1)/(y2 - y1). orjabinina