(Смотри рисунок). Дано: АВСД - трапеция ЕФ - средняя линия ЕФ1=12 ФФ1=6 угол 1=углу2 Найти S
Угол 1=углу3(как внутренние накрест лежащие при параллельных прямых ВС и АД и секущей ВД). Так как угол 3=углу2, то ΔВСД - равнобедренный и ВС=СД=АВ. ЕФ1 - средняя линия треугольника АВД ⇒ АД по свойству средней линии треугольника рана 2×12=24. ФФ1 - средняя линия треугольника ВСД ⇒ ВС=2×6=12. Значит СД и АВ равны 12. Найдем АН. ВС=НК=12. АН+КД=24-12=12. Так как трапеция равнобедренная, то АН=КД=12/2=6. Рассмотрим ΔАВН - прямоугольный. По теореме Пифагора ВН= Площадь трапеции - это средняя линя(которая равна 12+6=18)×высоту S=18×
Дано:
АВСД - трапеция
ЕФ - средняя линия
ЕФ1=12
ФФ1=6
угол 1=углу2
Найти S
Угол 1=углу3(как внутренние накрест лежащие при параллельных прямых ВС и АД и секущей ВД). Так как угол 3=углу2, то ΔВСД - равнобедренный и ВС=СД=АВ.
ЕФ1 - средняя линия треугольника АВД ⇒ АД по свойству средней линии треугольника рана 2×12=24.
ФФ1 - средняя линия треугольника ВСД ⇒ ВС=2×6=12.
Значит СД и АВ равны 12.
Найдем АН.
ВС=НК=12.
АН+КД=24-12=12.
Так как трапеция равнобедренная, то АН=КД=12/2=6.
Рассмотрим ΔАВН - прямоугольный.
По теореме Пифагора ВН=
Площадь трапеции - это средняя линя(которая равна 12+6=18)×высоту
S=18×
11.
Дано:
ΔАВС - равнобедренный
АС = ВС = 13
АВ = 10
Найти:
АС - высоту. опущенную на боковую сторону
СD - высота равнобедренного треугольника. опущенная на основание, является и медианой. Поэтому AD = BD = 0.5AB = 0.5 · 10 = 5.
По теореме Пифагора
АС² = CD² + AD²
13² = CD² + 5²
CD² = 13² - 5² = 144 = 12²
CD = 12
Площадь треугольника АВС
S = 0.5 CD · AB = 0.5 · 12 · 10 = 60
Площадь треугольника АВС можно также вычислить и так:
S = 0.5 BC · AE
откуда
АЕ = 2S : BC = 2 · 60 : 13 = 9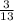
≈ 9.23
АЕ = 9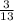
≈ 9.23
12.
Дано:
MKNR - ромб
KR = 10 - 1-я диагональ ромба
MN = 12 - 2-я диагональ ромба
Найти:
МК - сторону ромба
Пусть О - точка пересечения диагоналей ромба.
Диагонали ромба делятся точкой пересечения пополам, поэтому
КО = 0,5 KR = 0.5 · 10 = 5
МО = 0,5 MN = 0.5 · 12 = 6
Диагонали ромба пересекаются под прямым углом, поэтому
КО ⊥ МО и ΔМКО - прямоугольный с гипотенузой МК.
По теореме Пифагора
МК² = КО² + МО²
МК² = 5² + 6² = 61
МК = √61 ≈ 7,81
Сторона ромба МК =√61 ≈ 7,81