а) ∠L - прямой ⇒ ∠TEL = ∠L = 90° - как соответственные углы при ET║LK и секущей PL. Аналогично TN║PL - по условию ⇒ ∠LNT = ∠L = 90°,
∠ETN = ∠TEL = 90° - как пары соответственных углов ⇒ четырехугольник ETNL является прямоугольником (все углы прямые, стороны попарно параллельны)
б) Если прямая проходит через середину одной стороны треугольника параллельно другой стороне, то такая прямая является средней линией. В нашем случае (см. рисунок) ET║LK, TN║PL и Т - середина гипотенузы PK по условию ⇒ ET и TN - средние линии данного треугольника,
а значит, точки Е и N также делят пополам стороны Δ: точка Е делит пополам катет PL, а точка N - соответственно катет LK ⇒
ET = LN = , TN = EL = ⇒ периметр ETNL равен: Р = 4 + 4 + 3 + 3 = 8 + 6 = 14
№1 первый рисунок, на нем изображено то что дано.
Так как АВСD – параллелограмм, то АВ||CD, тогда угол DCN = угол
BNC как накрест-лежащие при паралельных прямых AB u CD и секущей CN.
CN – биссектриса по условию, значит угол DCN= угол BCN.
Исходя из равенств: угол BNC= угол DCN= угол BCN. Получим что ∆BNC – равнобедренный с основанием CN, так как углы при его основании равны.
У равнобедренного треугольника боковые стороны равны, следовательно BC=BN=4 см
Периметр параллелограмма это сумма двух его смежных сторон, умноженная на два. Тоесть:
P=(ВС+АВ)*2= (ВС+AN+BN)*2= (4+3+4)*2=22 см.
ответ: 22 см
№2 второй рисунок, на нем изображено то что дано
Та что е ABCD – параллелограмм, то АD||BC, тогда угол DAM= угол BMA как накрест-лежащие при паралельных прямых AD и BC и секущей АМ.
АМ – по условию биссектриса, значит угол DAM= угол BAM.
Исходя из ранее найденного: угол DAM= угол АМВ= угол ВАМ.
Тогда получим что, ∆ВАМ – равнобедренный с основанием АМ, так как углы при основании равны.
АВ=ВМ как боковые стороны равнобедренного треугольника, тогда АВ=5 см.
Периметр параллелограмма это сумма двух его смежных сторон, умноженная на два. Тоесть:
Р=(АВ+ВС)*2=(АВ+ВМ+СМ)*2= (5+5+6)*2= 32 см.
ответ: 32 см
а) ∠L - прямой ⇒ ∠TEL = ∠L = 90° - как соответственные углы при ET║LK и секущей PL. Аналогично TN║PL - по условию ⇒ ∠LNT = ∠L = 90°,
∠ETN = ∠TEL = 90° - как пары соответственных углов ⇒ четырехугольник ETNL является прямоугольником (все углы прямые, стороны попарно параллельны)
б) Если прямая проходит через середину одной стороны треугольника параллельно другой стороне, то такая прямая является средней линией. В нашем случае (см. рисунок) ET║LK, TN║PL и Т - середина гипотенузы PK по условию ⇒ ET и TN - средние линии данного треугольника,
а значит, точки Е и N также делят пополам стороны Δ: точка Е делит пополам катет PL, а точка N - соответственно катет LK ⇒
ET = LN =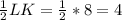
, TN = EL = 
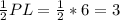⇒ периметр ETNL равен: Р = 4 + 4 + 3 + 3 = 8 + 6 = 14
ответ: периметр равен 14 см