Дано:
Вершины трапеции
А(3; -1; 2), В(1; 2; -1) и С(-1; 1; -3)
МК - средняя линия
Найти:
Уравнение средней линии МК
Составим уравнение прямой АВ
Таким образом, направляющий вектор прямой АВ
Проекции боковой стороны ВС на координатные оси равны
Найдём координаты точки К, принадлежащей боковой стороне ВС трапеции и, одновременно, средней линии.
Уравнение прямой МК, параллельной прямой АВ, то есть имеющей направляющий вектор и проходящей через точку К
Уравнение средней линии трапеции
Дано:
Вершины трапеции
А(3; -1; 2), В(1; 2; -1) и С(-1; 1; -3)
МК - средняя линия
Найти:
Уравнение средней линии МК
Составим уравнение прямой АВ
Таким образом, направляющий вектор прямой АВ
Проекции боковой стороны ВС на координатные оси равны
Найдём координаты точки К, принадлежащей боковой стороне ВС трапеции и, одновременно, средней линии.
Уравнение прямой МК, параллельной прямой АВ, то есть имеющей направляющий вектор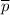 и проходящей через точку К
и проходящей через точку К
Уравнение средней линии трапеции