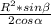Выясним, о каком многоугольнике речь. Из каждой вершины выпуклого n-угольника можно провести диагонали во все вершины , кроме 2-х смежных и самой себя, т.е. n-3 диагонали. Однако, любая диагональ из А в С есть одновременно и диагональ из С в А. Поэтому, у выпуклого n-угольника число диагоналей d=n·(n-3)/2. В то же время, по условиям задачи, у нашего многоугольника d=3n. Решаем уравнение: 3n=n·(n-3)/2; 6n=n²-3n; 9n=n²; n=9 Таким образом, речь идет о 9-угольнике. Поскольку правильный n-угольник можно представить, как n смыкающихся треугольников с общей вершиной, сумма всех внутренних углов правильного n-угольника равна n·180°-360°. В данном случае, для 9-угольника: 9·180°-360°=1260°
Через вершину конуса проведена плоскость под углом альфа к плоскости основания. Эта плоскость пересекает основание конуса по морде, которая видна из центра его основания под углом бета. Радиус основания R. Найдите площадь сечения.
Объяснение:
Образующие конуса равны , поэтому ΔABS равнобедренный. Пусть SK⊥AB, тогда ОК⊥АВ по т. О трех перпендикулярах.Т.к. ОА=ОВ как радиусы, то высота КО является биссектрисой ∠АОК=.
Из каждой вершины выпуклого n-угольника можно провести диагонали во все вершины , кроме 2-х смежных и самой себя, т.е. n-3 диагонали.
Однако, любая диагональ из А в С есть одновременно и диагональ из С в А. Поэтому, у выпуклого n-угольника число диагоналей d=n·(n-3)/2.
В то же время, по условиям задачи, у нашего многоугольника d=3n.
Решаем уравнение: 3n=n·(n-3)/2; 6n=n²-3n; 9n=n²; n=9
Таким образом, речь идет о 9-угольнике.
Поскольку правильный n-угольник можно представить, как n смыкающихся треугольников с общей вершиной, сумма всех внутренних углов правильного n-угольника равна n·180°-360°.
В данном случае, для 9-угольника: 9·180°-360°=1260°
Через вершину конуса проведена плоскость под углом альфа к плоскости основания. Эта плоскость пересекает основание конуса по морде, которая видна из центра его основания под углом бета. Радиус основания R. Найдите площадь сечения.
Объяснение:
Образующие конуса равны , поэтому ΔABS равнобедренный. Пусть SK⊥AB, тогда ОК⊥АВ по т. О трех перпендикулярах.Т.к. ОА=ОВ как радиусы, то высота КО является биссектрисой ∠АОК=
.
ΔАОК- прямоугольный ,
cos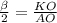
, KO=R*cos
;
sin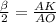
,AK=R*sin
,AB=α2Rsin
.
ΔSKO прямоугольный ,cos α=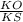
, KS=R*cos
/cosα.
S=0,5*AB*SK ,S=0,5*2R*sin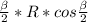
/ cosα,
S=0,5*R²*sinβ/cosα=