У чотирикутнику ABCD AB=CD, BC=AD, ∠A=30°. На стороні‎ BC позначено точку M так, шо ∠CDM=60°. Доведі‎ть, що чотирикутник ABMD -- рі‎внобі‎чна тропеці‎я.

По т .Пифагора  c²=a²+b²   у нас  a²+b² =17²=289     Р=2(а+b)=46 или 
(а+b)=46:2=23    решаем систему уравн.    a²+b² =289
                                                                         a+b=23    выразим а=23-b и подставим в первое уравнение   (23-b)²+b²=289
                                                        529-46b+b²+b²-289=0
                                                        2b²-46b+240=0    разделим на 2
                                                         b²-23b+120=0    D=23²-4*120=49
   b1=(23+√49)\2=(23+7) \2=30\2=15      b2=(23-7)\2=16\2=8
   a1=23-15=8      a2=23-8=15    отв. стороны прямоугольника 8 и 15 см.

Рассмотрим ΔABC - равнобедренный; AB=BC=25 см;

BD - медиана ⇒ AD=DC=14:2=7 см

Т.к. ΔABC - равнобедренный, то BD - является и высотой, и биссектрисой еще.

Рассмотрим ΔABD - прямоугольной; ∠D - прямой, AB=25см; AD=7 см

по т. Пифагора найдем BD

BD² = AB² - AD²

BD² = 25² - 7²

BD = 24 cм

Рассмотрим еще раз ΔABC:

по свойству медианы OD=1/3 * BD = 1/3 * 24 = 24 : 3 = 8 см

Рассмотрим ΔCOD - прямоугольный; ∠D - прямой; DC=7 см; OD=8 см

по т.Пифагора найдем OC

OC² = OD² + DC²

OC² = 8² + 7²

OC =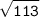 см

по свойству медианы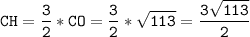 см

по свойству равнобедренного треугольника CH=AK=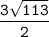 см

ответ: 24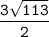 см; 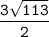 см;  см