Тело вращения представляет из себя цилиндр с высотой, равной меньшей стороне треугольника 13 см и радиусом оснований 16 см, из которого "вырезаны" усеченные конусы с равными радиусами и образующими 14 см и 15 см.
–––––––––––––––––––––––––––––––––––––––
Искомая площадь - сумма боковых поверхностей этих усеченных конусов S1+S2 и боковой поверхности цилиндра S3.
а) Для решения нужно найти радиус меньшей окружности, которая образуется при вращении вершины треугольника, противолежащей меньшей стороне.
Найдем высоту треугольника, проведенную к меньшей стороне, из его площади. Площадь треугольника со сторонами 13,14,15 встречается часто и равна 84 ( проверьте по ф.Герона)
Цилиндр, ось ОО1, сечение квадрат АВСД, дуга АД=60, диагональАС=а*корень2, АД=АВ=СД=АД=корень(АС в квадрате/2)=корень(2*а в квадрате/2)=а = высота цилиндра, проводим радиусы ОА=ОД, треугольник АОД, уголАОД-центральный опирается на дугу АД=дугеАД=60, треугольник АОД равносторонний, уголДАО=уголАДО=(180-уголАОД)/2=(180-60)/2=60, все углы=60, АД=ОА=ОД=а, площадь полной поверхности=2*пи*радиус*(радиус+высота)=2*пи*а*(а+а)=4пи*а в квадрате, проводим высоту ОН на АД=медиане=биссектрисе (можно построить треугольник на середине оси ОО1 =треугольнику АОД и провести высоту, то расстояние будут равны высоте ОН), уголАОН=уголАОД/2=60/2=30, ОН=ОА*cos30=а*корень3/2 =расстояние №1 здесь лучше рассматривать две плоскости одной из которых окружность с радиусом=5 и центом О, и ниже окружность с центом О1 вписанная в равносторонний треугольник со стороной 6*корень3 , радиус вписанной окружности=сторона*корень3/6=6*корень3*корень3/6=3, соединяем центры (-это перпендикуляр =расстояние от цента шара до плоскости треугольника) проводим радиус вписанной окружности в точку касания -О1А, проводим радиус шара ОА, треугольник О1ОА прямоугольный, ОА=5, О1А=3, ОО1=корень(ОА в квадрате-О1А в квадрате)=корень(25-9)=4
Тело вращения представляет из себя цилиндр с высотой, равной меньшей стороне треугольника 13 см и радиусом оснований 16 см, из которого "вырезаны" усеченные конусы с равными радиусами и образующими 14 см и 15 см.
–––––––––––––––––––––––––––––––––––––––
Искомая площадь - сумма боковых поверхностей этих усеченных конусов S1+S2 и боковой поверхности цилиндра S3.
а) Для решения нужно найти радиус меньшей окружности, которая образуется при вращении вершины треугольника, противолежащей меньшей стороне.
Найдем высоту треугольника, проведенную к меньшей стороне, из его площади. Площадь треугольника со сторонами 13,14,15 встречается часто и равна 84 ( проверьте по ф.Герона)
Высота равна 168:13=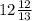 см
см
Радиус меньшей окружности равен R-h
Формула боковой поверхности усеченного конуса
Ѕ=πRL•(R+r)⇒
S1=π•14•(16+3,0769)=267,0766π см²
S2=π•15•(16+3,0769)=286,1535π см²
По формуле боковой поверхности цилиндра
S3=2πr•13=32•π•13=416π см²
S=969,2301π см² или ≈ 3044,926 см²