у людське око потрапляє 55 фотонів зеленого світла довжиною хвилі 550 нм за одну секунду. Визначіть потужність джерела світла що забезпечує таку чутливість ока.

Показать ответ

Ответ:

asadhfdgj

05.08.2021 23:08

Пусть дан треугольник АВС с прямым углом А, в котором проведена биссектриса АЕ, длину которой нужно найти.

Биссектриса треугольника делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам.

Запишем пропорцию:

$\rm{\dfrac{AB}{BE}= \dfrac{AC}{CE}}$

$\mathrm{\dfrac{AB}{AC}= \dfrac{BE}{CE}}=\dfrac{a}{b}$

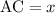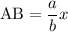Пусть $\mathrm{AC}=x$ . Тогда $\mathrm{AB}=\dfrac{a}{b} x$ .

Запишем теорему Пифагора для треугольника АВС:

$\rm{AB^2+AC^2=BC^2}$

$\left(\dfrac{a}{b} x\right)^2+x^2=(a+b)^2$

$\dfrac{a^2}{b^2}\cdot x^2+x^2=(a+b)^2$

$\left(\dfrac{a^2}{b^2}+1\right)\cdot x^2=(a+b)^2$

$x^2=\dfrac{(a+b)^2}{\dfrac{a^2}{b^2}+1}$

$x^2=\dfrac{b^2(a+b)^2}{a^2+b^2}$

$x=\dfrac{b(a+b)}{\sqrt{a^2+b^2} }$

Значит:

$\mathrm{AC}=\dfrac{b(a+b)}{\sqrt{a^2+b^2} }$

$\mathrm{AB}=\dfrac{a}{b}\cdot \dfrac{b(a+b)}{\sqrt{a^2+b^2} }=\dfrac{a(a+b)}{\sqrt{a^2+b^2} }$

Запишем теорему синусов для треугольника АЕС:

$\rm{\dfrac{AE}{\sin C} =\dfrac{EC}{\sin EAC} }$

Так как АЕ - биссектриса, то ЕАВ и ЕАС равны по половине прямого угла, то есть по 45°.

Синус угла С определим как отношение противолежащего катета к гипотенузе:

$\rm{\sin C=\dfrac{AB}{BC} }$

Теперь можем найти биссектрису:

$\rm{AE =\dfrac{EC\cdot\sin C}{\sin EAC} }$

$\rm{AE =\dfrac{EC\cdot AB }{BC \cdot\sin EAC} }$

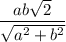
$\mathrm{AE} =\dfrac{b\cdot\dfrac{a(a+b)}{\sqrt{a^2+b^2} } }{(a+b) \cdot\sin 45^\circ}=\dfrac{\dfrac{ab}{\sqrt{a^2+b^2} } }{ \sin 45^\circ} }=\dfrac{\dfrac{ab}{\sqrt{a^2+b^2} } }{\dfrac{1}{\sqrt{2} } }=\dfrac{ab\sqrt{2}}{\sqrt{a^2+b^2}}$

ответ: $\dfrac{ab\sqrt{2}}{\sqrt{a^2+b^2}}$

Из вершины прямого угла проведена биссектриса, делящая гипотенузу на отрезки а и b. Чему равна эта б

0,0(0 оценок)

Ответ:

ХЗшкин

04.10.2021 11:04

Рисунок понимаешь вот какой)))
1) угол А+угол В=180 (градусов)-Т.К.соседние углы...
следовательно угол В=180-угол А=180-60=120
2)угол А=угол С=60; угол В=угол Д=120-Т. К. СВ-ВА РОМБА.
3)при пересечении диагоналей ромба образуется перпендикуляр,т.е. можно сказать,что треугольник будет прямоугольным (но это не обязательно писать)...
вообщем диагонали ромба являются биссектрисами и т.е. они делять углы пополам.
угол АВО = угол ОВС=120:2=60
угол ВСО = угол ДСО=60:2=30
4)рассмотрим треугольник ВОС
треугольник ВОС -прямоугольный,угол ВОС=90...Ну а дальше понятно.
ответ:угол ВОС=90;ОВС=60;ВСО=30

Вромбе abcd угол а равен 60 градусов диагонали ромба пересекаются в точке о найти углы треугольника