У паралелограмі abcd точка n належить стороні ab причому ab:bn=5:2. знайдіть відношення площі трикутника and до площі трикутника ncd

сделаем построение - сразу все видно

точки  K L M N - середины сторон прямоугольника АВСД

проведем прямые LN (параллельна АВ и СД) и КМ (параллельна ВС и АД)- 

они образуют равные прямоугольники  (стороны попарно равны)

KBLO  с диагональю KL

OLCM  с диагональю LM

NOMD  с диагональю NM

АKОN  с диагональю KN

и так понятно, что диагонали в равных прямоугольниках равны

KL=LM=NM=KN

но если кто сомневается , то можно доказать через теорему Пифагора

KL^2=KB^2+BL^2

LM^2=LC^2+CM^2

NM^2=MD^2+ND^2

KN^2=AN^2+AK^2

правые части этих выражений равны - это все половинки сторон

а значит равны и левые части

итак все стороны нового четырехугольника равны - это основное свойство РОМБА

если бы начальной фигурой был квадрат - то внутри тоже получился бы квадрат - но у нашего ромба углы 60-120-60-120

1. Могут.

2. б) 6 см

3. б) 45°

Объяснение:

1. Пересекающиеся прямые а и b задают плоскость α. Прямые а и с скрещивающиеся, значит прямая с не лежит в плоскости α.

Прямые с и b могут быть параллельными.

2.

а) Так как точки М и  N принадлежат плоскости трапеции и плоскости α, то MN - линия пересечения плоскостей.

MN - средняя линия трапеции, значит

AD║MN, ⇒  AD║α (если прямая параллельна некоторой прямой, лежащей в плоскости, то она параллельна плоскости).

б)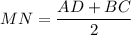

AD + BC = 2MN

BC = 2MN - AD = 2 · 8 - 10 = 16 - 10 = 6 см

3. Признак скрещивающихся прямых: если одна прямая лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то прямые скрещивающиеся.

а) ВС лежит в плоскости (АВС),

МА пересекает (АВС) в точке А,

А не лежит на прямой ВС, значит

МА и ВС скрещивающиеся.

б) ∠(МА, AD) = 45° по условию,

BC║AD, значит

∠(МА, ВС) = 45°