У прямокутний трикутник ABC вписано коло, ∠B — прямий. Обчисли кути трикутника A та C, а також кути, що виходять з центра кола, якщо один з них ∠ FOE = 130°.  Відповідь: ∠ A= ° ∠ C= ° ∠EOD = ° ∠DOF = °
1) члены предложения, относящиеся к одному и тому же члену предложения, отвечающие на один вопрос, выполняющие одинаковую синтаксическую функцию; 2) члены предложения, выделяемые по смыслу и интонационно; 3) все члены предложения, кроме подлежащего и сказуемого.
Обособленные обстоятельства выражаются одиночными деепричастиями или деепричастными оборотами, сравнительными оборотами, существительными в косвенных падежах с предлогами. Обособленные уточняющие обстоятельства могут быть также выражены наречиями.
Дополнения в предложении могут обособляться, а могут не обособляться – в зависимости от того, что хотел передать автор.
Чаще всего обособляются обороты, которые условно называются дополнениями, выраженными существительными с предлогами «кроме», «вместо», «за исключением», «исключая», «помимо» и др. Такие дополнения имеют расширительное или, наоборот, ограничительное значение: Поездка ей в целом понравилась, за исключением этих двух происшествий.
Сравнительные обороты интонируются в речи, а на письме обособляются – выделяются запятыми. 1. Сравнительные обороты, начинающиеся сравнительными союзами (как, будто, словно, точно, чем, нежели, как будто и др.), выделяются (или отделяются) запятыми.
Сравнительный оборот, образующий именную часть составного сказуемого, или тесно связанный со ним по смыслу, не обособляется: Пьеса написана как комедия. ... Сравнительный оборот, представляющий собой устойчивое сочетание, не обособляется: После этих слов он вскочил как ужаленный.
Объяснение:
Обособленными членами предложения называются:
1) члены предложения, относящиеся к одному и тому же члену предложения, отвечающие на один вопрос, выполняющие одинаковую синтаксическую функцию; 2) члены предложения, выделяемые по смыслу и интонационно; 3) все члены предложения, кроме подлежащего и сказуемого.
Обособленные обстоятельства выражаются одиночными деепричастиями или деепричастными оборотами, сравнительными оборотами, существительными в косвенных падежах с предлогами. Обособленные уточняющие обстоятельства могут быть также выражены наречиями.
Дополнения в предложении могут обособляться, а могут не обособляться – в зависимости от того, что хотел передать автор.
Чаще всего обособляются обороты, которые условно называются дополнениями, выраженными существительными с предлогами «кроме», «вместо», «за исключением», «исключая», «помимо» и др. Такие дополнения имеют расширительное или, наоборот, ограничительное значение: Поездка ей в целом понравилась, за исключением этих двух происшествий.
Сравнительные обороты интонируются в речи, а на письме обособляются – выделяются запятыми. 1. Сравнительные обороты, начинающиеся сравнительными союзами (как, будто, словно, точно, чем, нежели, как будто и др.), выделяются (или отделяются) запятыми.
Сравнительный оборот, образующий именную часть составного сказуемого, или тесно связанный со ним по смыслу, не обособляется: Пьеса написана как комедия. ... Сравнительный оборот, представляющий собой устойчивое сочетание, не обособляется: После этих слов он вскочил как ужаленный.
1.
Расстояние между точкой A & прямой a — проекция наклонной Ba, или просто — катет.
Другого определения здесь невозможно дать, этот треугольник обязательно должен быть прямоугольным.
<B = 30°; Теоерема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов — равен половине гипотенузы.
Напротив угла <B — лежит катет Aa, тоесть: Aa = Ba/2.
Катет Aa — мы можем найти только теоремой Пифагора:
Вывод: Aa = 2.31.
2.
<A = 90°; <B == <C => BA == AC.
BC (гипотенуза) = 14; по теореме Пифагора:
Нарисуем дополнительную высоту, проведённую через прямой угол: Высота AM.
В равнобедренном прямоугольном треугольнике — высота, проведённая к гипотенузе — это — и медиана, и высота, и биссектриса.
То есть: AM == MC = 14/2 (свойство медианы в прямоугольном треугольнике) = 7.
Вывод: AM = 7.
3.
<B = 30° => AC = BC/2 (теорема о 30-градусном угле).
Опять же, теорема Пифагора:
Высоту нарисуем дополнительную, в рисунке — её нет.
Добавим новую точку на гипотенузе BC — пусть будет — M.
Отрезок AM — это и есть расстояние между прямой a — и точкой A.
<MAC = 90 - <C = 90-60 = 30° => MC = AC/2 (теорема о 30-градусном угле).
MC = AC/2 => MC = 11.54/2 = 5.8.
По теореме Пифагора:
Вывод: MC = 9.99.
\\ВНИМАНИЕ!
Теорема Пифагора такова: Сумма квадратов катетов равна квадрату гипотенузы, тоесть: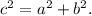 \\
\\