У прямокутному трикутнику ABC гiпотенуза AB Дорiвнюе 92см,кут B=30°.Знайдiть катет AC

1) Найдем площадь ромба.

Нам известны длины диагоналей ромба. Мы можем найти площадь ромба. Запишем формулу для площади:

S=1/2×d1×d2,

где d1 и d2 –диагонали ромба.

Подставив значения диагоналей в формулу, найдем площадь:

S=1/2×6×8=24 см².

2) Найдем сторону ромба.

Исходя из свойств ромба, зная диагонали, мы можем найти его сторону. Запишем:

Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4:

d1²+d2²=4a²,

где d1 и d2 –диагонали ромба, а – сторона ромба.

Подставив значения диагоналей в формулу, найдем сторону ромба:

6²+8²=4×а²,

4×а²=36+64,

4×а²=100,

а²=√(100:4),

а²=√25,

а=5 см.

3) Найдем высоту ромба. Запишем формулу для площади через сторону ромба и высоту:

S = ah,

где a — сторона ромба, h — высота.

Выразим из этой формулы высоту:

h=S:а.

Площадь и сторону ромба мы нашли, значит:

h=24:5=4,8 см.

ответ: высота ромба равна 4,8 см.

Стороны второго треугольника относятся как 9 : 4 : 7 и большая сторона равна 108 см.

Найдем остальные стороны.

9 частей — 108 см.

4 части — х см.

Составим пропорцию:

;

(см).

9 частей — 108 см.

7 частей — у см.

Составим пропорцию:

;

(см).

Значит, стороны второго треугольника равны 48 см, 84 см и 108 см.

Можем сделать вывод, что стороны первого и второго треугольника пропорциональны:

Значит, данные треугольники подобны по трем сторонам, и коэффициент подобия равен .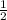

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Значит, S₁ : S₂ = .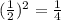

ответ: площади двух треугольников относятся как 1 : 4.