Через вершину конуса проведена плоскость под углом альфа к плоскости основания. Эта плоскость пересекает основание конуса по морде, которая видна из центра его основания под углом бета. Радиус основания R. Найдите площадь сечения.
Объяснение:
Образующие конуса равны , поэтому ΔABS равнобедренный. Пусть SK⊥AB, тогда ОК⊥АВ по т. О трех перпендикулярах.Т.к. ОА=ОВ как радиусы, то высота КО является биссектрисой ∠АОК=.
Прямые симметричны относительно ОС, поскольку усеченные круговые сегменты (один из них - СЕВ, ограничен дугой СВ) равны по площади, и оба равны четверти круга с вырезанным прямоугольным треугольником (справа это ОСЕ), следовательно, прямоугольные треугольники равны по площади, один катет у них общий, => они равны. Это - очевидно, но надо было это отметить.
Осталось понять, что 2*Scoe = Sceb = Socb - Scoe; :)
Через вершину конуса проведена плоскость под углом альфа к плоскости основания. Эта плоскость пересекает основание конуса по морде, которая видна из центра его основания под углом бета. Радиус основания R. Найдите площадь сечения.
Объяснение:
Образующие конуса равны , поэтому ΔABS равнобедренный. Пусть SK⊥AB, тогда ОК⊥АВ по т. О трех перпендикулярах.Т.к. ОА=ОВ как радиусы, то высота КО является биссектрисой ∠АОК=
.
ΔАОК- прямоугольный ,
cos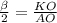
, KO=R*cos
;
sin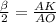
,AK=R*sin
,AB=α2Rsin
.
ΔSKO прямоугольный ,cos α=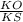
, KS=R*cos
/cosα.
S=0,5*AB*SK ,S=0,5*2R*sin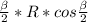
/ cosα,
S=0,5*R²*sinβ/cosα=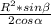
См. чертеж.
Прямые симметричны относительно ОС, поскольку усеченные круговые сегменты (один из них - СЕВ, ограничен дугой СВ) равны по площади, и оба равны четверти круга с вырезанным прямоугольным треугольником (справа это ОСЕ), следовательно, прямоугольные треугольники равны по площади, один катет у них общий, => они равны. Это - очевидно, но надо было это отметить.
Осталось понять, что 2*Scoe = Sceb = Socb - Scoe; :)
3*R*a/2 = pi*R^2/4;
ОЕ = а = pi*R/6; BE = R - a = R*(1 - pi/6);
Две прямые поделят диаметр на три отрезка
R*(1 - pi/6); pi*R/3; R*(1 - pi/6); ну, отсюда пропорция
(1 - pi/6) : (pi/3) : (1 - pi/6)