У рівнобедреному трикутнику ABC з основою АС кут при основі на 21° менший від кута при вершині, протилежній основі. Знайдіть кут при вершині цього трикутника. (У відповідь вкажіть лише число) *
Чтобы решать такие задачи, нужно уметь правильно определять, что есть наша прямая, что есть наклонная к нашей прямой, а что есть проекция наклонной.
4. В четвертой задаче у вас по условию дан уже прямой угол, от этого нужно отталкиваться.
Нам дан прямой угол между BC и AC, эти прямые обе лежат в плоскости нижнего треугольника, значит какая то из них будет являтся искомой прямой, а какая то будет проекцией наклонной на эту же плоскость нижнего треугольника. BC не может быть ничьей проекцией по рисунку, значит она будет являтся нашей прямой. Тогда AC
будет являться чьей-то проекцией. По рисунку видно, что AC будет являтся проекцией MC и MA перпендикуляр к плоскости ACB(если не понятны мои рассуждения, рекомендую разобраться, как строятся
наклонные и их проекции, а также разобраться и с самой теоремой о этих перпендикулярах).
Таким образом, зная все три прямые, можем применять теорему о трех перпендикулярах.
BC (наша прямая в плоскости) перпенд. AC (AC проекция MC) - по условию, значит BC также будет перпендикулярна и самой MC - по теореме.
Дальше просто техническая часть, находим BC из нижнего прямоугольного треугольника и применяем свойство синуса для нахождения гипотенузы MB в треуг. MCB.
5. В пятом задании необходимо правильно определить искомое расстояние, (как известно, расстояние это кратчайший путь, т.е перпендикуляр). Когда мы его проведем (пусть это будет MO),
он будет являтся нашей наклонной на плоскость ABC, далее необходмо будет провести проекцию данной наклонной в плоскости ABC. Так как MO - уже перпендикуляр к
AC, то и его проекция в плоскости также будет перпендикулярна к AC. Далее, похожая техническая часть 4-го задания, увидим в плоскости ABC необходмый прямоугольный треугольник,
применяя свойство синуса найдем катет. И в нашем искомом треугольнике также найдем сторону по Пифагору (зная, что MB перпендикуляр к плоскости).
1. Треугольники АВС и MNK подобны. ∠А = ∠М. ВС = 8, NK = 2. Площадь треугольника MNK равна 12 (ед²). Найдите площадь треугольника АВС.- - -
Дано :
ΔАВС ~ ΔMNK.
∠А = ∠М.
ВС = 8.
NK = 2.
S(ΔMNK) = 12 (ед²).
Найти :
S(ΔABC) = ?
В подобных треугольниках против равных углов лежат сходственные стороны.
Отсюда стороны ВС и NK - сходственные.
Отношение сходственных сторон равно коэффициенту подобия.
То есть -
Но заметить, ища коэффициент подобия, я ставила в числитель элемент бóльшего треугольника. Поэтому при дальнейших расчётах, я буду также ставить элементы/площадь бóльшего треугольника в числитель.
Площади подобных треугольников относятся как квадрат коэффициента подобия.
В треугольнике параллельный одной из сторон треугольника отрезок, пересекающий две другие стороны треугольника в точках, отсекает от данного треугольника подобный треугольник.
Отсюда -
ΔАВС ~ ΔMBK.
В подобных треугольниках против равных углов лежат сходственные стороны. И их же отношение равно коэффициенту подобия.
∠В - общий для ΔАВС и ΔMBK.
Отсюда стороны МК и АС - сходственные.
Тогда -
Периметры подобных треугольников относятся как коэффициент подобия.
Объяснение:
Чтобы решать такие задачи, нужно уметь правильно определять, что есть наша прямая, что есть наклонная к нашей прямой, а что есть проекция наклонной.
4. В четвертой задаче у вас по условию дан уже прямой угол, от этого нужно отталкиваться.
Нам дан прямой угол между BC и AC, эти прямые обе лежат в плоскости нижнего треугольника, значит какая то из них будет являтся искомой прямой, а какая то будет проекцией наклонной на эту же плоскость нижнего треугольника. BC не может быть ничьей проекцией по рисунку, значит она будет являтся нашей прямой. Тогда AC
будет являться чьей-то проекцией. По рисунку видно, что AC будет являтся проекцией MC и MA перпендикуляр к плоскости ACB(если не понятны мои рассуждения, рекомендую разобраться, как строятся
наклонные и их проекции, а также разобраться и с самой теоремой о этих перпендикулярах).
Таким образом, зная все три прямые, можем применять теорему о трех перпендикулярах.
BC (наша прямая в плоскости) перпенд. AC (AC проекция MC) - по условию, значит BC также будет перпендикулярна и самой MC - по теореме.
Дальше просто техническая часть, находим BC из нижнего прямоугольного треугольника и применяем свойство синуса для нахождения гипотенузы MB в треуг. MCB.
5. В пятом задании необходимо правильно определить искомое расстояние, (как известно, расстояние это кратчайший путь, т.е перпендикуляр). Когда мы его проведем (пусть это будет MO),
он будет являтся нашей наклонной на плоскость ABC, далее необходмо будет провести проекцию данной наклонной в плоскости ABC. Так как MO - уже перпендикуляр к
AC, то и его проекция в плоскости также будет перпендикулярна к AC. Далее, похожая техническая часть 4-го задания, увидим в плоскости ABC необходмый прямоугольный треугольник,
применяя свойство синуса найдем катет. И в нашем искомом треугольнике также найдем сторону по Пифагору (зная, что MB перпендикуляр к плоскости).
P.S Делать нечего на третьем курсе физмата <3
Дано :
ΔАВС ~ ΔMNK.
∠А = ∠М.
ВС = 8.
NK = 2.
S(ΔMNK) = 12 (ед²).
Найти :
S(ΔABC) = ?
В подобных треугольниках против равных углов лежат сходственные стороны.Отсюда стороны ВС и NK - сходственные.
Отношение сходственных сторон равно коэффициенту подобия.То есть -
Но заметить, ища коэффициент подобия, я ставила в числитель элемент бóльшего треугольника. Поэтому при дальнейших расчётах, я буду также ставить элементы/площадь бóльшего треугольника в числитель.
Площади подобных треугольников относятся как квадрат коэффициента подобия.Отсюда -
192 (ед²).
- - -2. В треугольнике АВС отрезок MК (М ∈ АВ, К ∈ ВС) параллелен АС. МК = 14, АС = 42. Периметр треугольника МВК равен 32. Найдите периметр треугольника АВС.- - -Дано :
ΔАВС.
М ∈ АВ, К ∈ ВС.
МК ║АС.
МК = 14.
АС = 42.
Р(ΔМВК) = 32.
Найти :
Р(ΔАВС) = ?
В треугольнике параллельный одной из сторон треугольника отрезок, пересекающий две другие стороны треугольника в точках, отсекает от данного треугольника подобный треугольник.Отсюда -
ΔАВС ~ ΔMBK.
В подобных треугольниках против равных углов лежат сходственные стороны. И их же отношение равно коэффициенту подобия.∠В - общий для ΔАВС и ΔMBK.
Отсюда стороны МК и АС - сходственные.
Тогда -
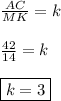
Периметры подобных треугольников относятся как коэффициент подобия.Отсюда -
96.