1. Соединим точки С и D с центром. Тогда треугольники AOD и ВОС равнобедренные (OA = OB = OC = OD как радиусы), ⇒
∠1 = ∠2 и ∠3 = ∠4.
∠2 = ∠3 как накрест лежащие при пересечении параллельных прямых AD и ВС секущей АВ. Но тогда в этих треугольниках равны и углы при вершине О. Значит треугольники AOD и ВОС равны по двум сторонам и углу между ними, ⇒
AD = BC.
2. Точки, находящиеся на данном расстоянии от данной прямой а, будут расположены на прямой, параллельной прямой а (красные прямые). В зависимости от расположения прямых задача может иметь одно решение (1), два решения (2) и не иметь решения (3).
2) Прямая призма состоит из 6 поверхностей: двух совершенно одинаковых оснований и 3-х боковых сторон. Самое простое сначала вычислить площадь основания призмы. Так как это прямоугольный треугольник, то вычисляется по формуле половина произведения его катетов. То есть 0,5*3*4=6 см. Каждая боковая сторона вычисляется отдельно как площадь прямоугольника. Площадь AA1B1B равняется произведению высоты призмы на сторону AB. 4*10=40 см2. Площадь BB1CC1 равна произведению стороны BC на высоту призмы, то есть 3*10=30 см2. Чтобы вычислить сторону призмы ACC1A1 над вычислить по теореме Пифагора сторону AC. . AC=5 см. Значит площадь третьей боковой стороны равна произведению высоты призмы на сторону AC. 5*10=50 см2. Значит площадь всей поверхности призмы равна
S=132 cм2.
1) Площадь поверности октаэдра состоит из 8 равносторонних треугольников. Достаточновычислить площадь одного из равносторонних треугольников и помножить все то на 8. Так как сторона одного из этих треугольников равна 1 см, то, вспомнив, что в равностороннем треугольнике все углы равны и они по 60 градусов каждый, то можно вычислить с формулы , где - угол между сторонами a и b. Значит . . Теперь умножим эту площадь на 8. Получим .
1. Соединим точки С и D с центром. Тогда треугольники AOD и ВОС равнобедренные (OA = OB = OC = OD как радиусы), ⇒
∠1 = ∠2 и ∠3 = ∠4.
∠2 = ∠3 как накрест лежащие при пересечении параллельных прямых AD и ВС секущей АВ. Но тогда в этих треугольниках равны и углы при вершине О. Значит треугольники AOD и ВОС равны по двум сторонам и углу между ними, ⇒
AD = BC.
2. Точки, находящиеся на данном расстоянии от данной прямой а, будут расположены на прямой, параллельной прямой а (красные прямые). В зависимости от расположения прямых задача может иметь одно решение (1), два решения (2) и не иметь решения (3).
2) Прямая призма состоит из 6 поверхностей: двух совершенно одинаковых оснований и 3-х боковых сторон. Самое простое сначала вычислить площадь основания призмы. Так как это прямоугольный треугольник, то вычисляется по формуле половина произведения его катетов. То есть 0,5*3*4=6 см. Каждая боковая сторона вычисляется отдельно как площадь прямоугольника. Площадь AA1B1B равняется произведению высоты призмы на сторону AB. 4*10=40 см2. Площадь BB1CC1 равна произведению стороны BC на высоту призмы, то есть 3*10=30 см2. Чтобы вычислить сторону призмы ACC1A1 над вычислить по теореме Пифагора сторону AC.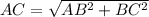
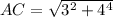 . AC=5 см. Значит площадь третьей боковой стороны равна произведению высоты призмы на сторону AC. 5*10=50 см2. Значит площадь всей поверхности призмы равна
. AC=5 см. Значит площадь третьей боковой стороны равна произведению высоты призмы на сторону AC. 5*10=50 см2. Значит площадь всей поверхности призмы равна
1) Площадь поверности октаэдра состоит из 8 равносторонних треугольников. Достаточновычислить площадь одного из равносторонних треугольников и помножить все то на 8. Так как сторона одного из этих треугольников равна 1 см, то, вспомнив, что в равностороннем треугольнике все углы равны и они по 60 градусов каждый, то можно вычислить с формулы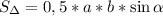 , где
, где 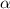 - угол между сторонами a и b. Значит
- угол между сторонами a и b. Значит 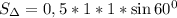 .
. 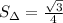
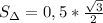 . Теперь умножим эту площадь на 8. Получим
. Теперь умножим эту площадь на 8. Получим 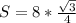
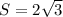 .
.