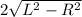У рівнобедреному трикутнику АВС з основою АС проведено висоту ВD. Знайдіть периметр трикутника АВС, якщо ВD = 7 см, а периметр трикутника АВD дорівнює 34 см)
Будь Ласка ть. ів

Сосны, земля и расстряние между верхушками составляют прямоугольную трапецию. где сосны – основания, а земля и расстояние между верхушками – боковые стороны.проведем высоту из вершины тупого угла(верхушка короткой сосны), она разделит прямоугольную трапецию на прямоугольник и прямоугольный треугольник. где высота равна 16метров (расстояние между соснами).если основания трапеции равны 27метров и 15метров, тогда катет прямоугольного треугольника равен высоте трапеции, а второй катет 27 - 15 = 12метроврасстояние между верхушками – боковая сторона трапеции и гипотенуза одновременно.сумма квадратов катетов равно квадрату гипотенузы12² + 16² = 144+256=400√400 = 20метров.

Объяснение:

Дано: Окр.О,R;

MO = L

MB₁, MB₂, A₂A₁ - касательные.

Найти: Р (ΔА₁МА₂)

1. Рассмотрим ΔОМВ₁.

Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ОВ₁ ⊥ МВ₁ ⇒ ΔОМВ₁ - прямоугольный.

По теореме Пифагора найдем МВ₁ :

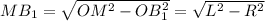
2. Отрезки касательных к окружности, проведённые из одной точки, равны.

⇒ МВ₁ = МВ₂ =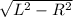

3. Рассмотрим ΔА₁МА₂

Р (ΔА₁МА₂) = А₂М + МА₁ + А₁А₂

А₁А₂ = А₁С + СА₂

А₂С = А₂В₂ ;  СА₁ = А₁В₁ (отрезки касательных)

Тогда:

Р (ΔА₁МА₂) = А₂М + МА₁ + А₁С + СА₂ = А₂М + МА₁ + А₁В₁ + А₂В₂

А₂М + А₂В₂ = МВ₂

МА₁ + А₁В₁ = МВ₁

⇒ Р (ΔА₁МА₂)  = МВ₂ + МВ₁ =