ответ:1.1 а) свойство острых углов в прямоугольном треугольнике
1.2 в
1.3 а) катет прямоугольного треугольника лежащий против угла в 30° равен половине гипотензия
1.4 а) если катет прямоугольного треугольникаравен половине гипотензы, то угол, лежащий против этого катета равен 30°
2 : а) если катеты одного прямоугольного треугольника соответственно равны
катетам другого то такие треугольники равны
б) если гипотенза и острый угол одного прямоугольного треугольника соответственно равны гипотезе и острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны
в) если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему углу другого, то такие треугольники равны
д) если гипотенза и острый угол одного прямоугольного треугольника соответственно равны гипотензе и острому углу другого, то такие треугольники равны
е) если гипотенза и катет одного прямоугольного треугольника соответственно равны гипотенза же и катету другого, то такие треугольники равны
15) Цена за билет для одного школьника составляет рублей (умножаем на 80 потому, что при скидке 20% от первоначальной цены билета остаётся 100-20=80%). Значит, для четырёх школьников цена составит рублей.
16) MN - средняя линия треугольника ABC, так как из условия MN || BC и AM = MB. Отсюда BC = 2MN, AM = 0.5AB, AN = 0.5AC. Периметр треугольника AMN по этим утверждениям можно записать следующим образом: . Вынеся одинаковый множитель за скобку, получим: , а так как выражение в скобках - это данный нам периметр, то периметр треугольника AMN можно выразить как половину периметра треугольника ABC, то есть, 32.
17) Угол DBC равен углу ADB (как внутренние накрест лежащие при параллельных прямых BC и AD и секущей BD). Отсюда, угол DBC составляет 34°. Значит, целиком угол B составляет (48+34)° = 82°.
18) Расстояние от точки до прямой - это перпендикуляр к этой прямой. Точка пересечения диагоналей прямоугольника лежит на прямой, на которой находится его средняя линия. Получаем, что наше расстояние параллельно сторонам BC и AD прямоугольника и равно половине любой из этих сторон. Отсюда BC = AD = 8*2 = 16 см. Площадь прямоугольника ABCD равна 12*16 = 192 см².
19) , значит, отрезок нижнего основания от высоты до ближайшей боковой стороны равен 3 см. Так как высота, точка которой совпадает с началом либо концом меньшего основания, отсекает от трапеции прямоугольный треугольник с катетами, равными высоте и найденному только что отрезку, и гипотенузой, равной боковой стороне. Катет, лежащий против угла в 30 градусов, равен половине гипотенузы, отсюда боковая сторона равна 3*2 = 6 см. Периметр трапеции будет составлять 11+6+5+6=28 см.
20) Угол BMC равен углу ABM как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BM. Значит, треугольник BCM - равнобедренный, откуда CM = CB = 12 см. Периметр параллелограмма ABCD будет равен 2*(12+(12+5)) = 58 см. Такой же ответ получим, если предположим, что угол B - тупой и пересечение с боковой стороной падает на продолжение этой стороны.
ответ:1.1 а) свойство острых углов в прямоугольном треугольнике
1.2 в
1.3 а) катет прямоугольного треугольника лежащий против угла в 30° равен половине гипотензия
1.4 а) если катет прямоугольного треугольникаравен половине гипотензы, то угол, лежащий против этого катета равен 30°
2 : а) если катеты одного прямоугольного треугольника соответственно равны
катетам другого то такие треугольники равны
б) если гипотенза и острый угол одного прямоугольного треугольника соответственно равны гипотезе и острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны
в) если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему углу другого, то такие треугольники равны
д) если гипотенза и острый угол одного прямоугольного треугольника соответственно равны гипотензе и острому углу другого, то такие треугольники равны
е) если гипотенза и катет одного прямоугольного треугольника соответственно равны гипотенза же и катету другого, то такие треугольники равны
ж) тоже самое как и в е)
Объяснение:
Объяснение:
15) Цена за билет для одного школьника составляет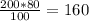 рублей (умножаем на 80 потому, что при скидке 20% от первоначальной цены билета остаётся 100-20=80%). Значит, для четырёх школьников цена составит
рублей (умножаем на 80 потому, что при скидке 20% от первоначальной цены билета остаётся 100-20=80%). Значит, для четырёх школьников цена составит 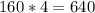 рублей.
рублей.
16) MN - средняя линия треугольника ABC, так как из условия MN || BC и AM = MB. Отсюда BC = 2MN, AM = 0.5AB, AN = 0.5AC. Периметр треугольника AMN по этим утверждениям можно записать следующим образом: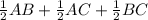 . Вынеся одинаковый множитель за скобку, получим:
. Вынеся одинаковый множитель за скобку, получим: 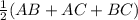 , а так как выражение в скобках - это данный нам периметр, то периметр треугольника AMN можно выразить как половину периметра треугольника ABC, то есть, 32.
, а так как выражение в скобках - это данный нам периметр, то периметр треугольника AMN можно выразить как половину периметра треугольника ABC, то есть, 32.
17) Угол DBC равен углу ADB (как внутренние накрест лежащие при параллельных прямых BC и AD и секущей BD). Отсюда, угол DBC составляет 34°. Значит, целиком угол B составляет (48+34)° = 82°.
18) Расстояние от точки до прямой - это перпендикуляр к этой прямой. Точка пересечения диагоналей прямоугольника лежит на прямой, на которой находится его средняя линия. Получаем, что наше расстояние параллельно сторонам BC и AD прямоугольника и равно половине любой из этих сторон. Отсюда BC = AD = 8*2 = 16 см. Площадь прямоугольника ABCD равна 12*16 = 192 см².
19)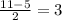 , значит, отрезок нижнего основания от высоты до ближайшей боковой стороны равен 3 см. Так как высота, точка которой совпадает с началом либо концом меньшего основания, отсекает от трапеции прямоугольный треугольник с катетами, равными высоте и найденному только что отрезку, и гипотенузой, равной боковой стороне. Катет, лежащий против угла в 30 градусов, равен половине гипотенузы, отсюда боковая сторона равна 3*2 = 6 см. Периметр трапеции будет составлять 11+6+5+6=28 см.
, значит, отрезок нижнего основания от высоты до ближайшей боковой стороны равен 3 см. Так как высота, точка которой совпадает с началом либо концом меньшего основания, отсекает от трапеции прямоугольный треугольник с катетами, равными высоте и найденному только что отрезку, и гипотенузой, равной боковой стороне. Катет, лежащий против угла в 30 градусов, равен половине гипотенузы, отсюда боковая сторона равна 3*2 = 6 см. Периметр трапеции будет составлять 11+6+5+6=28 см.
20) Угол BMC равен углу ABM как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BM. Значит, треугольник BCM - равнобедренный, откуда CM = CB = 12 см. Периметр параллелограмма ABCD будет равен 2*(12+(12+5)) = 58 см. Такой же ответ получим, если предположим, что угол B - тупой и пересечение с боковой стороной падает на продолжение этой стороны.