Раз призма правильная треугольная, значит в основании лежит правильный треугольник.
Площадь правильного треугольника рассчитывается по формуле:
Сторона основания - это и есть сторона правильного треугольника. Значит, а = 6.
Площадь одного основания будет равна:
Таких оснований в призме два, значит сумма их площадей будет равна:
=
Боковая поверхность призмы складывается из площадей трех четырехугольников. Площадь каждого четырехугольника равна произведению высоты призмы на сторону основания: h*a = 6*h.
Площадь боковой поверхности призмы арвна:
3*6*h = 18*h.
площадь боковой поверхности призмы равна сумме площадей ее оснований. Приравниваем обе суммы, получаем уравнение:
= 18*h.
Решаем уравнение:
h = .
Высота, то есть длина бокового ребра призмы равна .
Так как в условии сказано "В треугольнике постройте точку", а треугольник - это плоская фигура, то значит надо построить точку ВНУТРИ треугольника. Точка, равноудаленная от сторон треугольника - это центр вписанной окружности. Этот центр лежит на пересечении биссектрис треугольника. Таким образом, надо построить треугольник по трем сторонам, а затем построить биссектрисы двух углов (достаточно). Точка пересечения этих биссектрис и даст нам искомую точку. Для построения на прямой "а" откладываем сторону АС треугольника (например, равную 7см) и из точек А и С проводим дуги окружностей радиусами 5см и 6см соответственно. Пересечение этих дуг даст нам точку В (вершину треугольника). Теперь делим углы А и С пополам. Для этого проводим окружности с центрами в точках А и С так, чтобы получить точки пересечения D и E, F и G этих окружностей со сторонами АВ и АС, СВ и АС соответственно. Из точек D и E, F и G проводим дуги окружностей радиусами DE и FG, соответственно и соединив полученные точки пересечения окружностей, получаем искомые биссектрисы и точку O их пересечения. Это и есть искомая точка, равноудаленная от сторон треугольника.
Расстояние от найденной точки до сторон треугольника (радиус вписанной окружности) можно найти по формуле: r=S/p, где S - площадь треугольника, а р - его полупериметр. У нас p = (5+6+7):2=9. S=√[p(p-a)(p-b)(p-c)] = √(9*2*3*4)=6√6. r=6√6/9=2√6/3≈1,6см.
Раз призма правильная треугольная, значит в основании лежит правильный треугольник.
Площадь правильного треугольника рассчитывается по формуле:
Сторона основания - это и есть сторона правильного треугольника. Значит, а = 6.
Площадь одного основания будет равна:
Таких оснований в призме два, значит сумма их площадей будет равна:
Боковая поверхность призмы складывается из площадей трех четырехугольников. Площадь каждого четырехугольника равна произведению высоты призмы на сторону основания: h*a = 6*h.
Площадь боковой поверхности призмы арвна:
3*6*h = 18*h.
площадь боковой поверхности призмы равна сумме площадей ее оснований. Приравниваем обе суммы, получаем уравнение:
Решаем уравнение:
h =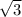 .
.
Высота, то есть длина бокового ребра призмы равна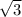 .
.
Для построения на прямой "а" откладываем сторону АС треугольника (например, равную 7см) и из точек А и С проводим дуги окружностей радиусами 5см и 6см соответственно. Пересечение этих дуг даст нам точку В (вершину треугольника). Теперь делим углы А и С пополам. Для этого проводим окружности с центрами в точках А и С так, чтобы получить точки пересечения D и E, F и G этих окружностей со сторонами АВ и АС, СВ и АС соответственно. Из точек D и E, F и G проводим дуги окружностей радиусами DE и FG, соответственно и соединив полученные точки пересечения окружностей, получаем искомые биссектрисы и точку O их пересечения. Это и есть искомая точка, равноудаленная от сторон треугольника.
Расстояние от найденной точки до сторон треугольника (радиус вписанной окружности) можно найти по формуле: r=S/p, где S - площадь треугольника, а
р - его полупериметр. У нас p = (5+6+7):2=9.
S=√[p(p-a)(p-b)(p-c)] = √(9*2*3*4)=6√6.
r=6√6/9=2√6/3≈1,6см.