У трикутниках АВС і А1В1С1: кут А=куту А1, кут С=куту С1; АС=А1С1=6 см, ВС=2 см, А1В1=7 см. Доведіть рівність трикутників і знайдіть периметр трикутника АВС.​

Я это понимаю так: На отрезках АМ и МВ, как на сторонах, построены квадраты АМСД и МВЕF... Далее то тексту.

В прямоугольных треугольниках АМF и СМВ катеты FМ=МВ и АМ=СМ, значит тр-ки равны. ∠МСВ=∠FАМ.
В тр-ке СМВ ∠МСВ+∠СВМ=90°, значит ∠NАВ+∠NВА=90°, значит тр-ник АNВ - прямоугольный.
Треугольники АNВ и МСВ подобны по трём углам, значит NВ/МВ=АN/СМ, но СМ=АМ ⇒ NВ/МВ=АN/АМ. В тр-ке АNВ это тождество соответствует утверждению теоремы биссектрис, значит NМ - биссектриса тр-ка АNВ.
Во вписанном в окружность прямоугольном треугольнике АNВ АВ - диаметр, биссектриса АМ пересекает окружность в точке S, причём ∩AS=∩BS, так как на них опираются равные вписанные углы ANS и BNS.
Таким образом, точка S - середина дуги АВ. Это будет работать всегда, при любом положении точки М на отрезке АВ. Т.к. АВ - всегда диаметр одинаковой окружности, все прямые MN проходят через точку S.
Доказано.

Ці точки лежать на серединному перпендикулярі точок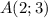 та 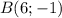. Знайдемо координати точки — середини відрізка :

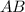Щоб знайти кутовий коефицієнт серединного перпендикуляра, знайдемо кутовий коефіцієнт прямої :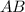

Коефіцієнт перпендикулярної прямої дорівнює . Застосуємо формулу прямої за кутовим коефицієнтом і точкою, через яку пряма проходить:

Тобто серединний перпендикуляр має формулу .

Знайдемо точку його перетину:

а) З віссю абсцисс:

Тобто точка має координати (3; 0).

б) З віссю ординат:

Все зобразив на графіку. Перемалюйте його в зошит, щоб отримати вищу оцінку ;)

Відповідь:

а) (3; 0)

б) (0; –3)