У трикутнику центр вописаного кола лежить на медіані. доведіть, що цей трикутник рівнобедрений

Так, подібні. У ромба всі сторони рівні. Якщо провести меншу діагональ, то ми отримаємо ромб, який складається з двох правильних (рівносторонніх) трикутників. Будь-які правильні трикутники подібні (за трьома сторонами). Тому подібними є і конструкції з двох таких трикутників.

P. S. Якщо вже доводити максимально строго: у правильного трикутника кут дорівнює 60°. Тому в цього ромба кути дорівнюють 120°, 60°, 120°, 60°, а всі сторони рівні. Якщо у двох чотирикутників рівні всі відповідні кути, а відповідні сторони пропорційні, то вони подібні.

1. Рассмотрим треугольник ABD

∠ BAD = 90° (как угол прямоугольника) => треугольник ABD прямоугольный, BD - гипотенуза

По теореме Пифагора находим катет AD:

см

BC = AD = 8 см (как стороны прямоугольника)

AB = DC = 6 см (как стороны прямоугольника)

2. Проведём AP. Треугольник ABP - прямоугольный, т.к. прямая BP ⊥ AB (т. к. перпендикулярна плоскости прямоугольника ABCD) по условию.

По теореме Пифагора находим гипотенузу AP:

см

3. Проведём прямую PD и рассмотрим треугольник PAD

По теореме о трёх перпендикулярах PA ⊥ AD

(т.к. PB ⊥ AD (т.к. ⊥ плоскости) и AB ⊥ AD (как смежные стороны прямоугольника) )

(PB - перпендикуляр, PA - наклонная, BA - проекция наклонной)

∠PAD = 90° =>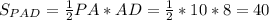 см²

4. Проведём PC. Треугольник BPC - прямоугольный, т.к. прямая BP⊥BC (т.к. ⊥ плоскости прямоугольника ABCD) по условию.

По теореме Пифагора находим гипотенузу PC:

см

5. Рассмотрим треугольник PDC

По теореме о трёх перпендикулярах PC ⊥ DC

(т.к. PB ⊥ DC (т.к. ⊥ плоскости) и BC ⊥ CD (как смежные стороны прямоугольника) )

(PB - перпендикуляр, PC - наклонная, BC - проекция наклонной)

∠PCD = 90° =>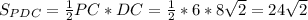 см²

ответ: Площадь треугольника PAD = 40 см²; Площадь треугольника PDC = 24√2 см²