Сумма острых углов прямоугольного треугольника равна 90°.
=>∠ЕВС = 90° - 70° = 20°
Так как ЕВ - биссектриса, по условию => ∠АВС = 20° × 2 = 40°
=> ∠САВ = 90° - 40° = 50°
ответ: 50°.
Так как АВ = ВС => ∆АВС - равнобедренный.
∠А = ∠С, по свойству равнобедренного треугольника.
Сумма углов треугольника равна 180°.
180° - 120° = 60° - сумма ∠А и ∠С.
∠А = ∠С = 60 ÷ 2 = 30°
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> АН = 4 ÷ 2 = 2 см.
ответ: 2 см.
Если катет равен половине гипотенузы, то напротив лежащий угол равен 30°.
=> ∠CAD = 30°
Так как AD = AB = 7 см => ∆ABD - равнобедренный.
=> ∠D = 90° - 30° = 60°
∠D = ∠B = 60°, по свойству равнобедренного треугольника.
=> ∠А = 180° - (60° + 60°) = 60°
Вывод: ∆BAD - равносторонний (все углы равны по 60°)
ответ: 60°, 60°.
=> ∠КСВ = 30°
Так как СК - биссектриса, по условию => ∠АСК = 30°
∠ВСА = 30° × 2 = 60°
=> ∠ВАС = 90° - 60° = 30°.
Сумма смежных углов равна 180°.
∠ВАС смежный с ∠CAD => ∠CAD = 180° - 30° = 150°.
ответ: 150°.
Рассмотрим ∆АСР и ∆РВС:
АС = РВ, по условию.
СВ - общая сторона.
=> ∆АСР = ∆РВС, по катетам.
=> ∠А = ∠Р.
Ч.Т.Д.
На рисунке изображён рисунок к 1 задаче (изначально точка Е не была дана)
3) Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Так как углы, взятые в порядке следования относятся как 1:3:4 , то ∠А=х , ∠В=3х , ∠С=4х и ∠А+∠С=х+4х=5х=180° , х=36° .
∠А=36° , ∠В=3*36°=108° , ∠С=4*36°=144°
Сумма внутренних углов четырёхугольника равна 360°.
∠D=360°-36°-108°-144°=72°
Или ∠В+∠D=5х , ∠D=5x-∠B=3x-3x=2x , 2x=2*36°=72° .
4) Сторона правильного треугольника равна .
Радиус вписанной окружности в прав. тр-к равна 1/3 его высоты, то есть .
Сторона прав.четырёхугольника - квадрата, описанного около окружности, равна .
Периметр квадрата равен см.
Сумма острых углов прямоугольного треугольника равна 90°.
=>∠ЕВС = 90° - 70° = 20°
Так как ЕВ - биссектриса, по условию => ∠АВС = 20° × 2 = 40°
Сумма острых углов прямоугольного треугольника равна 90°.
=> ∠САВ = 90° - 40° = 50°
ответ: 50°.
Задача#2.Так как АВ = ВС => ∆АВС - равнобедренный.
∠А = ∠С, по свойству равнобедренного треугольника.
Сумма углов треугольника равна 180°.
180° - 120° = 60° - сумма ∠А и ∠С.
∠А = ∠С = 60 ÷ 2 = 30°
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> АН = 4 ÷ 2 = 2 см.
ответ: 2 см.
Задача#3.Если катет равен половине гипотенузы, то напротив лежащий угол равен 30°.
=> ∠CAD = 30°
Так как AD = AB = 7 см => ∆ABD - равнобедренный.
Сумма острых углов прямоугольного треугольника равна 90°.
=> ∠D = 90° - 30° = 60°
∠D = ∠B = 60°, по свойству равнобедренного треугольника.
Сумма углов треугольника равна 180°.
=> ∠А = 180° - (60° + 60°) = 60°
Вывод: ∆BAD - равносторонний (все углы равны по 60°)
ответ: 60°, 60°.
Задача#4.Если катет равен половине гипотенузы, то напротив лежащий угол равен 30°.
=> ∠КСВ = 30°
Так как СК - биссектриса, по условию => ∠АСК = 30°
∠ВСА = 30° × 2 = 60°
Сумма острых углов прямоугольного треугольника равна 90°.
=> ∠ВАС = 90° - 60° = 30°.
Сумма смежных углов равна 180°.
∠ВАС смежный с ∠CAD => ∠CAD = 180° - 30° = 150°.
ответ: 150°.
Задача#5.Рассмотрим ∆АСР и ∆РВС:
АС = РВ, по условию.
СВ - общая сторона.
=> ∆АСР = ∆РВС, по катетам.
=> ∠А = ∠Р.
Ч.Т.Д.
На рисунке изображён рисунок к 1 задаче (изначально точка Е не была дана)
3) Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Так как углы, взятые в порядке следования относятся как 1:3:4 , то ∠А=х , ∠В=3х , ∠С=4х и ∠А+∠С=х+4х=5х=180° , х=36° .
∠А=36° , ∠В=3*36°=108° , ∠С=4*36°=144°
Сумма внутренних углов четырёхугольника равна 360°.
∠D=360°-36°-108°-144°=72°
Или ∠В+∠D=5х , ∠D=5x-∠B=3x-3x=2x , 2x=2*36°=72° .
4) Сторона правильного треугольника равна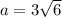 .
.
Радиус вписанной окружности в прав. тр-к равна 1/3 его высоты, то есть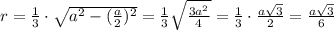 .
.
Сторона прав.четырёхугольника - квадрата, описанного около окружности, равна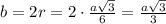 .
.
Периметр квадрата равен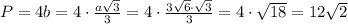 см.
см.