1) Боковое ребро образует с плоскостью основания угол 45 градусов следовательно угол АВС(обозначимего так, угол которойнаверху) тоже равен 45 градусов. Следовательно, ВЫСОТА пирамиды=Радиус описанной окружности.
2)Обозначим ВЫСОТУ=РАДИУС ОПИС.ОКР. через х. По т.Пифагора найдем х:
ВЫСОТА=РАДИУС.ОПИС.Окр.=
3) Радиус описанной окружности = диагональ квадрата разделить на 2 (В основании квадрат т.к. пирамида 4-х угольная и правильная)
Отсюда, диагональ квадрата =
4)Сторона квадрата=диагональ кв. делить на корень из 2= 4см
5)Площадь основания = сторона в квадрате=16 см^2
6)бок.поверхн-ть = 1/2 * Периметр основания * высота =
ABCD основание,S вершина, O центр основания(точка пересечения диагоналей), A вершина пирамиды, то угол SAO=45 гр., тогда SO(высота)=4*sin 45=2*sqrt(2), AO=SO=2*sqrt(2)(тр.SAO равнобедр.,два равных угла), сторона основания по т. Пифагора AB^2=AO^2+BO^2=8+8=16, AB=4(диагонали квадрата перпенд., равны и в точке пересечения делятся пополам)
Найдем апофему боковой грани.SK апофема, SK перпенд.CD,K середина CD,OK перпенд.CD, OK=2( половине стороны)
1) Боковое ребро образует с плоскостью основания угол 45 градусов следовательно угол АВС(обозначимего так, угол которойнаверху) тоже равен 45 градусов. Следовательно, ВЫСОТА пирамиды=Радиус описанной окружности.
2)Обозначим ВЫСОТУ=РАДИУС ОПИС.ОКР. через х. По т.Пифагора найдем х:
ВЫСОТА=РАДИУС.ОПИС.Окр.=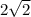
3) Радиус описанной окружности = диагональ квадрата разделить на 2 (В основании квадрат т.к. пирамида 4-х угольная и правильная)
Отсюда, диагональ квадрата =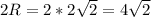
4)Сторона квадрата=диагональ кв. делить на корень из 2= 4см
5)Площадь основания = сторона в квадрате=16 см^2
6)бок.поверхн-ть = 1/2 * Периметр основания * высота =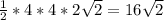
7)Площадь полной поверхности=16+16 кореньиз 2
ABCD основание,S вершина, O центр основания(точка пересечения диагоналей), A вершина пирамиды, то угол SAO=45 гр., тогда SO(высота)=4*sin 45=2*sqrt(2), AO=SO=2*sqrt(2)(тр.SAO равнобедр.,два равных угла), сторона основания по т. Пифагора AB^2=AO^2+BO^2=8+8=16, AB=4(диагонали квадрата перпенд., равны и в точке пересечения делятся пополам)
Найдем апофему боковой грани.SK апофема, SK перпенд.CD,K середина CD,OK перпенд.CD, OK=2( половине стороны)
SK^2=4+8=12
SK=2*sqrt(3)
S=3*SK*DC/2=3*2sqrt(3)*4/2=12*sqrt(3)