Формула линейной функции имеет вид y=kx+b, где х — независимая переменная (абсцисса точки); y — зависимая переменная (ордината точки); k, b — числовые коэффициенты.
Числовой коэффициент b показывает, в какой точке график пересекает ось ординат (Оу). В данном случае b = 3. Наша формула обретет вид:
Числовой коэффициент k отвечает за наклон графика линейной ф-ции:
Если график ф-ции образует с положительной осью Ox острый угол, тогда коэффициент k > 0, если тупой — k < 0.
В данном случае k < 0, то есть k — отрицательное число.
Из формулы выразим k:
Возьмём любую удобную нам точку на прямой и подставим ее координаты в полученную формулу:
A (4; 0)
В итоге, формула линейной функции получится следующей:
Примем коэффициент отношения отрезков на АВ равным а,Так как AM : MB = 3:4, то АВ=АМ+ВМ=7а ⇒ AM:AB = 3:7.
CN:CB = 3:7- дано.
а) Точки М и N лежат в плоскости ∆ АВС и в плоскости α. ⇒MN - линия пересечения этих плоскостей.
МN и АС высекают на прямых АВ и ВС пропорциональные отрезки.
Из обобщённой теоремы Фалеса: если отрезки, высекаемые прямыми на одной прямой, пропорциональны отрезкам, высекаемым теми же прямыми на другой прямой, то эти прямые параллельны.⇒ АС║MN.
Если прямая (АС), не лежащая в плоскости α, параллельна некоторой прямой (MN), которая лежит в плоскости α, то прямая параллельна плоскости . ⇒АС || α
б) Т.к. MN║AC, углы при их пересечении секущими АВ с одной стороны и ВС с другой равны как соответственные. Отсюда следует подобие треугольников MBN и ABC с коэффициентом подобия k=BC:NC=7:3 ⇒ AC:MN=7:3
Формула линейной функции имеет вид y=kx+b, где х — независимая переменная (абсцисса точки); y — зависимая переменная (ордината точки); k, b — числовые коэффициенты.
Числовой коэффициент b показывает, в какой точке график пересекает ось ординат (Оу). В данном случае b = 3. Наша формула обретет вид:
Числовой коэффициент k отвечает за наклон графика линейной ф-ции:
Если график ф-ции образует с положительной осью Ox острый угол, тогда коэффициент k > 0, если тупой — k < 0.
В данном случае k < 0, то есть k — отрицательное число.
Из формулы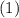
выразим k:
Возьмём любую удобную нам точку на прямой и подставим ее координаты в полученную формулу:
A (4; 0)В итоге, формула линейной функции получится следующей:
AC:16=7:3––АС=16•7:3=28 см
Объяснение:
Примем коэффициент отношения отрезков на АВ равным а,Так как AM : MB = 3:4, то АВ=АМ+ВМ=7а ⇒ AM:AB = 3:7.
CN:CB = 3:7- дано.
а) Точки М и N лежат в плоскости ∆ АВС и в плоскости α. ⇒MN - линия пересечения этих плоскостей.
МN и АС высекают на прямых АВ и ВС пропорциональные отрезки.
Из обобщённой теоремы Фалеса: если отрезки, высекаемые прямыми на одной прямой, пропорциональны отрезкам, высекаемым теми же прямыми на другой прямой, то эти прямые параллельны.⇒ АС║MN.
Если прямая (АС), не лежащая в плоскости α, параллельна некоторой прямой (MN), которая лежит в плоскости α, то прямая параллельна плоскости . ⇒АС || α
б) Т.к. MN║AC, углы при их пересечении секущими АВ с одной стороны и ВС с другой равны как соответственные. Отсюда следует подобие треугольников MBN и ABC с коэффициентом подобия k=BC:NC=7:3 ⇒ AC:MN=7:3
AC:16=7:3––АС=16•7:3=28 см