УМОЛЯ Найдите градусную величину вписанного угла в окружность, если величина центрального угла, опирающегося на ту же дугу, что и вписанный угол, равна 140.
В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)= =9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
=√3 см
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
=√147 см
Боковые грани правильной пирамиды это равные треугольники.
Тут надо исходить из того, что сумма 2-х сторон треугольника должна быть больше третьей стороне. 98+28=126(см), значит третья сторона должна быть меньше 126см,если взять за интервал измерений 1 см, (т.е. если не учитывать, что есть еще мм, и доли мм), то третья сторона максимально равна 125см. Тогда периметр 126+125=251(см). С другой стороны, если сторона 98см наибольшая в треугольнике, то сумма двух сторон должна быть больше 98, тогда 98-28=70(см). 28+71=99. Тогда периметр может быть равен 98+99=197(см) Короче периметр треугольника может принимать любые значения в интервале от 251см до 197см.
В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)=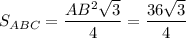 =9√3 см².
=9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
Боковые грани правильной пирамиды это равные треугольники.
S(бок.)=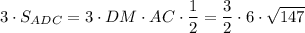 =9√147 см²
=9√147 см²
S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²
ответ: 9√3 + 9√147 см².
Тогда периметр 126+125=251(см).
С другой стороны, если сторона 98см наибольшая в треугольнике, то сумма двух сторон должна быть больше 98, тогда 98-28=70(см).
28+71=99. Тогда периметр может быть равен 98+99=197(см)
Короче периметр треугольника может принимать любые значения в интервале от 251см до 197см.