умоляю осталось 15 минут чтобы решить задачу решить эту задачу Напишите данные доказательства и так далее 16 упражнение не берите из интернета из одной точки проведены две касательные к окружности Докажите что отрезки касательных МР и МQ равны ​

Дано:

усеченный конус

r = O₁B = 5 см

R = OA = 11 см

см

-----------------------------

Найти:

Sсеч - ?

1) Проведем BH⊥AO.

  OH = O₁B = r = 5 см

  AH = OA - OH = R - r = 11 см - 5 см = 6 см

2) Рассмотрим ΔAHB:

   BH⊥AO        |  ⇒ ΔAHB - прямоугольный

   ∠AHB = 90° |

   AB² = AH² + HB² - по теореме Пифагора, следовательно: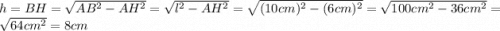h = BH = OO₁ = 8 см

3) Равнобедренная трапеция ABCD является осевым сечением данного усеченного конуса: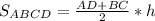

4) В трапеции ABCD:

   AD = 2AO = 2R = 2×11 см = 22 см      h = BH= 8 см

   BC = 2BO₁ = 2r = 2×5 см = 10 см

5) Тогда площадь трапеции равна:

⇒

Sсеч =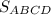 = 128 см²

ответ: Sсеч = 128 см²

P.S. Рисунок показан внизу↓

1) Дано:

<СВА = <DBA

DB = CB.

Док-ть:

∆АСВ = ∆ADB

Док-во:

Рассмотрим ∆АСВ и ∆ADB.

АВ - общая сторона.

<СВА = <DBA, DB = CB, значит ∆АСВ = ∆ADB по | признаку (по двум сторонам и углу между ними).

5) Дано:

QK = FP, QM = MP, KM = MF

<KQM = <FPM

Док-ть:

∆QFM = ∆KMP;

∆QKM = ∆FMP;

∆QPK = ∆QPF;

∆KQF = ∆KFP;

Док-во:

QK = FP, QM = MP, KM = MF, значит КQFP - параллелограмм.

<KQM = <FPM

1) Рассмотрим ∆QFM и ∆KMP.

<KMP = <QMP как вертикальные

QM = MP, KM = MF, значит ∆QFM = ∆KMP по | признаку.

QF = KP по св-ву параллелограмма, значит ∆QFM = ∆KMP по ||| признаку.

∆QFM = ∆KMP по | и ||| признакам.

2) Рассмотрим ∆FMP и ∆QMK.

<FMP = <QMK как вертикальные.

QK = FP, KM = MF, QM = MP, значит ∆FMP = ∆QMK по | и ||| признакам.

3) Рассмотрим ∆KQP и ∆QFP.

QK = FP, QP - общая сторона

KP = QF по св-ву параллелограмма.

<KQM = <FPM

<QKP = <QFP по св-ву параллелограмма, значит ∆KQP = ∆QFP по | , || , ||| признакам.

4) Рассмотрим ∆KQF и ∆KFP.

KF - общая сторона.

QK = FP, QF = KP.

<KQF = <FPK.

∆KQF и ∆KFP по | , || , ||| признакам.

ч.т.д