Плоскость, пересекающая ось цилиндра, пересекает основания цилиндра по хордам, длины которых равны 6 и 8. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра, если диаметр основания равен 10, а образующая 14.
Объяснение:
Радиус 10:2=5. Т.к. образующая 14, то ОО₁=14 .
Пусть ОМ=х, тогда МО₁ =14-х.
1) а)Пусть ОС⊥АВ. Тогда ОС в равнобедренном ΔАОВ, является медианой и АС=1/2АВ=1/2*6=3
В ΔАСО-прямоугольном , по т. Пифагора СО=√(5²-3²)=4
б)Пусть О₁С₁⊥А₁В₁. Тогда О₁₁С в равнобедренном ΔА₁О₁В₁ , является медианой и А₁С₁=1/2А₁В₁=1/2*8=4
В ΔА₁С₁О₁-прямоугольном , по т. Пифагора С₁О₁=√(5²-4²)=3.
2) Т.к. основания цилиндра параллельны, то ΔСОМ∼ ΔС₁О₁М по 2-м углам(∠СМО=∠С₁МО₁ как вертикальные, ∠СОМ=∠С₁О₁ М как соответственные) ⇒ сходственные стороны пропорциональны,
, 7х=14*4 , х=8. Поэтому МО₁ =14-8=6.
3) Линейным углом между плоскостью сечения и основанием будет ∠МС₁О₁ :
т.к. если проекция С₁О₁ ⊥А₁В₁ , то и наклонная МС₁⊥А₁В₁ .
Объяснение:
Плоскость, пересекающая ось цилиндра, пересекает основания цилиндра по хордам, длины которых равны 6 и 8. Найдите тангенс угла между этой плоскостью и плоскостью основания цилиндра, если диаметр основания равен 10, а образующая 14.
Объяснение:
Радиус 10:2=5. Т.к. образующая 14, то ОО₁=14 .
Пусть ОМ=х, тогда МО₁ =14-х.
1) а)Пусть ОС⊥АВ. Тогда ОС в равнобедренном ΔАОВ, является медианой и АС=1/2АВ=1/2*6=3
В ΔАСО-прямоугольном , по т. Пифагора СО=√(5²-3²)=4
б)Пусть О₁С₁⊥А₁В₁. Тогда О₁₁С в равнобедренном ΔА₁О₁В₁ , является медианой и А₁С₁=1/2А₁В₁=1/2*8=4
В ΔА₁С₁О₁-прямоугольном , по т. Пифагора С₁О₁=√(5²-4²)=3.
2) Т.к. основания цилиндра параллельны, то ΔСОМ∼ ΔС₁О₁М по 2-м углам(∠СМО=∠С₁МО₁ как вертикальные, ∠СОМ=∠С₁О₁ М как соответственные) ⇒ сходственные стороны пропорциональны,
3) Линейным углом между плоскостью сечения и основанием будет ∠МС₁О₁ :
т.к. если проекция С₁О₁ ⊥А₁В₁ , то и наклонная МС₁⊥А₁В₁ .
ΔМО₁С₁ -прямоугольный, tg∠МС₁О₁ =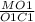
=
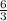⇒ tg∠МС₁О₁=2.
1200√3 см²
Объяснение:
Дано: КСМТ - трапеція, КС=МТ, ∠КМТ=90°, КМ - бісектриса, ОМ=КО=ОТ=40 см. Знайти S(КСМТ).
∠КМТ - прямий, отже він спирається на діаметр описаного кола, тоді КТ=КО+ОТ=80 см.
∠СКМ=∠ТКМ за умовою, ∠СМК=∠ТКМ як внутрішні при СМ║КТ і січній КМ, отже ∠КСМ=∠СКМ, а ΔКСМ - рівнобедрений, КС=СМ.
Проведемо радіус ОМ=40 см, ΔКОМ=ΔКСМ за двома кутами і спільною стороною, отже КС=СМ=КО=ОМ=40 см.
МТ=КС=40 см.
ΔОМТ - рівнобедрений, проведемо МН - висоту і медіану.
ОН=ТН=40:2=20 см
За теоремою Піфагора МН=√(МТ²-ТН²)=√(1600-400)=√1200=20√3 см.
S(КСМТ)=(СМ+КТ):2*МН=(40+80):2*20√3=1200√3 см²