Объяснение:
Вычисляем центр диагонали 0А по формуле
: S=(XB+XA)/2 ; (YB+YA)/2
S(OA)=(0+5)/2 ; (5+0)/2 = (5/2;5/2) = (2,5 ; 2,5)
Рассчитаем центр диагонали BО
S(BC)=(1+xB)/2 ; 3+yB)/2
* мы заменяем x и y на x и y z S(OA) (5/2;5/2)
(1+xB)/2=2,5 I *2 ; (3+yB)/2=2,5 I* 2
1+xB=5 3+yB=5
xB=5-1 yB=5-3
xB=4 yB=2
OTBET: Точка поиска B = (4; 2)
(w załączeniu grafik)
ответ: см³.
Дано:
Равнобедренный треугольник вращается вокруг высоты.
Высота проведена к основанию равнобедренного треугольника.
см.
-----------------------------------------------
При вращении равнобедренного треугольника вокруг высоты, образовался конус. Значит нам нужно найти объём конуса.
Высота является по свойству равнобедренного треугольника медианой и биссектрисой см.
Теперь найдём высоту по теореме Пифагора (, где и - катеты, - гипотенуза):
Затем найдём объём образовавшегося конуса:
см³.
Объяснение:
Вычисляем центр диагонали 0А по формуле
: S=(XB+XA)/2 ; (YB+YA)/2
S(OA)=(0+5)/2 ; (5+0)/2 = (5/2;5/2) = (2,5 ; 2,5)
Рассчитаем центр диагонали BО
S(BC)=(1+xB)/2 ; 3+yB)/2
* мы заменяем x и y на x и y z S(OA) (5/2;5/2)
(1+xB)/2=2,5 I *2 ; (3+yB)/2=2,5 I* 2
1+xB=5 3+yB=5
xB=5-1 yB=5-3
xB=4 yB=2
OTBET: Точка поиска B = (4; 2)
(w załączeniu grafik)
ответ: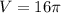 см³.
см³.
Объяснение:
Дано:
Равнобедренный треугольник вращается вокруг высоты.
Высота проведена к основанию равнобедренного треугольника.
-----------------------------------------------
При вращении равнобедренного треугольника вокруг высоты, образовался конус. Значит нам нужно найти объём конуса.
Высота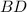 является по свойству равнобедренного треугольника медианой и биссектрисой
является по свойству равнобедренного треугольника медианой и биссектрисой 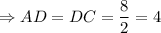 см.
см.
Теперь найдём высоту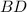 по теореме Пифагора (
по теореме Пифагора (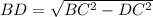 , где
, где 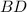 и
и 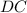 - катеты,
- катеты, 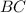 - гипотенуза):
- гипотенуза):
Затем найдём объём образовавшегося конуса: