1. Так как 15 < 12 + 9, треугольник с такими сторонами существует. Сравним квадрат большей стороны с суммой квадратов двух других сторон: 15² и 12² + 9² 225 и 144 + 81 225 = 225, значит по теореме, обратной теореме Пифагора, треугольник ответ: в) прямоугольный.
2. Коэффициент подобия: k = 2/5. Площади подобных треугольников относятся как квадрат коэффициента подобия: S₁ : S₂ = 4 : 25 8 : S₂ = 4 : 25 S₂ = 25 · 8 : 4 = 50 ответ: Нет правильного ответа.
3. АВ = ВС = (Рabc - AC) / 2 = (32 - 12) / 2 = 20 / 2 = 10 см Найдем площадь по формуле Герона (р - полупериметр): Sabc = √(p·(p - AB)·(p - BC)·(p - AC)) Sabc = √(16 · 6 · 6 · 4) = 4 · 6 · 2 = 48 см² Из другой формулы площади найдем радиус вписанной окружности: Sabc = p·r r = Sabc / p = 48 / 16 = 3 см ответ: б) 3 см
4. Проведем радиусы в точки касания. Отрезки касательных, проведенных из одной точки, равны: АК = АМ = 5 см, ВК = ВЕ = 12 см СМОЕ - квадрат со стороной, равной радиусу вписанной окружности, который обозначим r. По теореме Пифагора составим уравнение: (5 + 12)² = (5 + r)² + (12 + r)² 17² = 25 + 10r + r² + 144 + 24r + r² 2r² + 34r + 169 = 289 r² + 17r - 60 = 0 D = 289 + 240 = 529 r = (- 17 + 23) / 2 = 6 / 2 = 3 Второй корень отрицательный, не подходит по смыслу задачи. АС = 5 + 3 = 8 см ВС = 12 + 3 = 15 см ответ: г) 8 см и 15 см.
5. Центр окружности, описанной около прямоугольника, лежит в точке пересечения его диагоналей, значит радиус равен половине диагонали, которую находим по теореме Пифагора: r = d/2 = √(a² + k²) / 2
Поскольку четырехугольная пирамида ПРАВИЛЬНАЯ, то в основании лежит квадрат. Диагональ квадрата ABCD равен см. Диагонали квадрата пересекаются в точке О и точка О делит диагонали пополам, то есть см.
Из прямоугольного треугольника SOD: из определения косинуса найдем боковое ребро пирамиды:
см.
Высота SK равнобедренного треугольника SCD делит основание CD пополам, то есть: см
Тогда из прямоугольного треугольника SKC:
см. Тогда площадь грани SCD равна см²
Площадь боковой поверхности - это сумма всех площади граней. То есть, зная что у правильной пирамиды все грани равны, то площадь бок. пов.
Так как 15 < 12 + 9, треугольник с такими сторонами существует.
Сравним квадрат большей стороны с суммой квадратов двух других сторон:
15² и 12² + 9²
225 и 144 + 81
225 = 225, значит по теореме, обратной теореме Пифагора, треугольник
ответ: в) прямоугольный.
2.
Коэффициент подобия: k = 2/5.
Площади подобных треугольников относятся как квадрат коэффициента подобия:
S₁ : S₂ = 4 : 25
8 : S₂ = 4 : 25
S₂ = 25 · 8 : 4 = 50
ответ: Нет правильного ответа.
3.
АВ = ВС = (Рabc - AC) / 2 = (32 - 12) / 2 = 20 / 2 = 10 см
Найдем площадь по формуле Герона (р - полупериметр):
Sabc = √(p·(p - AB)·(p - BC)·(p - AC))
Sabc = √(16 · 6 · 6 · 4) = 4 · 6 · 2 = 48 см²
Из другой формулы площади найдем радиус вписанной окружности:
Sabc = p·r
r = Sabc / p = 48 / 16 = 3 см
ответ: б) 3 см
4.
Проведем радиусы в точки касания.
Отрезки касательных, проведенных из одной точки, равны:
АК = АМ = 5 см,
ВК = ВЕ = 12 см
СМОЕ - квадрат со стороной, равной радиусу вписанной окружности, который обозначим r.
По теореме Пифагора составим уравнение:
(5 + 12)² = (5 + r)² + (12 + r)²
17² = 25 + 10r + r² + 144 + 24r + r²
2r² + 34r + 169 = 289
r² + 17r - 60 = 0
D = 289 + 240 = 529
r = (- 17 + 23) / 2 = 6 / 2 = 3
Второй корень отрицательный, не подходит по смыслу задачи.
АС = 5 + 3 = 8 см
ВС = 12 + 3 = 15 см
ответ: г) 8 см и 15 см.
5.
Центр окружности, описанной около прямоугольника, лежит в точке пересечения его диагоналей, значит радиус равен половине диагонали, которую находим по теореме Пифагора:
r = d/2 = √(a² + k²) / 2
Поскольку четырехугольная пирамида ПРАВИЛЬНАЯ, то в основании лежит квадрат. Диагональ квадрата ABCD равен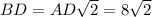 см. Диагонали квадрата пересекаются в точке О и точка О делит диагонали пополам, то есть
см. Диагонали квадрата пересекаются в точке О и точка О делит диагонали пополам, то есть 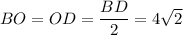 см.
см.
Из прямоугольного треугольника SOD: из определения косинуса найдем боковое ребро пирамиды:
Высота SK равнобедренного треугольника SCD делит основание CD пополам, то есть: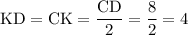 см
см
Тогда из прямоугольного треугольника SKC:
Площадь боковой поверхности - это сумма всех площади граней. То есть, зная что у правильной пирамиды все грани равны, то площадь бок. пов.
ответ: 64√3 см².