Утверждение вертикальные углы равны сформулируйте в форме: если то сформулируйте обратное ему утверждение верно ли оно

Показать ответ

Ответ:

9872105

27.04.2023 14:25

1рассмотрим треугольник aoc и треугольник bod: угол aoc = bod (как вертикальные) ao=ob и co=od (по условию,т.к. точка является o - посередине) значит, треугольник aoc = равен треугольнику bod (по двум сторонам и углу между ними) значит угол dao = равен углу cbo(в равных треугольниках против равных сторон лежат равные углы) 2 рассмотрим треугольник abd и треугольник adc: по условию, угол bda = углу adc сторона ad - общая и по условию угол bad = углу dac (т.к. ad - биссектриса) значит, треугольник abd = треугольнику adc(по двум углам и стороне между ними) значит сторона ab=ac(т.к. в равных треугольниках против равных углов лежат равны стороны)

0,0(0 оценок)

Ответ:

Zavgorodnev04

30.03.2022 16:43

66° и 42°

Объяснение:

Дано: Окр.О;

АВСD - вписанный четырехугольник;

АС ∩ BD = M; AB ∩ BC = N;

∠АMD = 108°; ∠AND = 24°.

Найти: ∠АBD и ∠BDC.

Угол между пересекающимися хордами окружности равен полусумме двух противоположных дуг, высекаемых этими хордами.

⇒

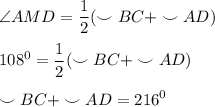$\displaystyle \angle{AMD}= \frac{1}{2} (\smile {BC}+\smile{AD})\\\\108^0=\frac{1}{2} (\smile {BC}+\smile{AD})\\\\\smile {BC}+\smile{AD}=216^0$ (1)

Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.

⇒

$\displaystyle \angle{AND}=\frac{1}{2}(\smile {AD}-\smile {BC})\\\\24^0= \frac{1}{2}(\smile {AD}-\smile {BC})\\\\48^0=\smile {AD}-\smile {BC}$ (2)

Из (2) выразим дугу AD и подставим в (1):

$\displaystyle \smile {AD}=48^0+\smile {BC}\\\\216^0=48^0+\smile {BC}+\smile {BC}\\\\2\smile {BC}=216^0-48^0\\\\\smile {BC}=84^0\\\\\smile {AD}=48^0+84^0=132^0$