Увыпуклого шестиугольника две пары противоположных стороны попарно равны и параллельны. докажите, что оставшиеся стороны также равны и параллельны.

Показать ответ

Ответ:

Angelina8672

04.11.2021 11:45

1)Диагональ квадрата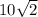 $10\sqrt{2}$

2)Такого правильного многоугольника не существует

3)Периметр ромба 60

Объяснение:

1)Сторона квадрата это два радиуса, то есть a = 2r = 2 * 5 = 10

По теореме Пифагора, диагональ =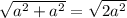 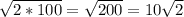$\sqrt{a^{2}+a^{2} }=\sqrt{2a^{2} }$ = $\sqrt{2 * 100} =\sqrt{200} =10\sqrt{2}$ , где а - сторона квадрата

2) Сумма улов n-угольника s = 180(n - 2)

1600 = 180(n - 2);

1600 = 180n - 360;

1960 = 180n;

196 = 18n;

n = 10,8 а так как n не является натуральным числом то такого многоугольника не существует

3)Так ромб частный случай паралеллограмма то его диагонали точкой пересечения делятся пополам, а свойству ромба его диагонали перпендикулярны, тогда по теореме Пифагора a =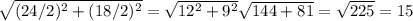 $\sqrt{(24 /2)^{2} +(18/2)^{2} } =\sqrt{12^{2} +9^{2} }\sqrt{144+81}=\sqrt{225}=15$

(a - сторона ромба )

По свойству ромба все его стороны равны тогда P ромба = 4a

= 4 * 15 = 60

0,0(0 оценок)

Ответ:

dimasikPro2

24.04.2023 03:39

Назовем трапецию ABCD, а высоту ВН. Проведем еще одну высоту из ∠С: СМ
Рассмотрим ΔАВН и ΔMCD:
AB=CD(по опр. равнобедренной трапеции)
∠ВНА=∠CMD=90(по опр. высоты)
∠А=∠D(по св-ву равнобедренной трапеции)
ВН=СМ(так как ВС параллельно AD⇒расстояние между ними всегда одинаковое, а оно измеряется посредством высот)
∠АВН=∠МСD(так как ∠В=∠С(по опр. равноб. трап.), а ∠НВС=∠МСВ=90(как накрест лежащие углы при параллельных прямых ⇒ ∠В - ∠НВС=∠С - ∠МСВ)
⇒ΔАВН = ΔMCD(по двум сторонам и углу между ними)
⇒АН=МD(как соответственные элементы в равных Δ)⇒АН=МD=6
Найдем основания:
AD=30+6=36
ВС=36-(6+6)=24 (Другими словами, мы из АD вычли отрезки MD и АН)

0,0(0 оценок)

Популярные вопросы: Геометрия