В. 45. угольной,
а высота
сованного
1 таблицу
значение
А. 30°.
з
-го угла,
гранями
17.15).
ате угої
Всь..
ной пи-
Найдите
А. 30.
С. 60°.
D. 90°.
3. Для куба ABCDA,B,C,D, найдите угол между прямыми BD и СА:
В. 45°.
С. 60°.
D. 90°.
4. Для куба ABCDA,B,C,D, найдите косинус угла между прямыми AA,
и DB:
1
А.
В.
С.
2.
D.
3
2
5. Найдите угол между скрещивающимися ребрами правильной тре-
угольной пирамиды:
А. 30°.
В. 45°.
С. 60°.
D. 90°.
6. Найдите угол между скрещивающимися ребрами правильной че-
тырехугольной пирамиды, все ребра которой равны 1:
А. 30°.
В. 45°.
С. 60°.
D. 90°.
7. Для правильной шестиугольной призмы ABCDEFA,B,C,D,E,F,
найдите угол между прямыми BC и CD.:
А. 30°.
В. 45°.
С. 60°.
D. 120°.
8. Пля правильной шестиҮгольной призмы ABCDEFA,B,C,D,E,F, най-
разован-
ранями
Inne

Показать ответ

Ответ:

аннасукманова020508

28.06.2022 08:14

Объяснение:

Раз нам даны точки в пространстве, то скорее всего с векторами уже знакомы, тогда. Найдем векторы АВ и ВС, для этого нужно от координат конца отнять соответствующие координаты начала, тогда

(в)АВ(-5-2;4-5;-4-(-1))=(-7;-1;-3)

(в)BC(1-(-5);-2-4;2-(-4))=(6,-6,6)

По определению параллелограма это четырехугольник у которого 2 пары параллельных равных сторон, сделовательно (в)AB=(в)CD

(в)AB(-7;-1;-3), C(1;-2;2) Пусть точка D имеет координаты x,y,z. Следовательно (в)CD(x-1;y+2;z-2) и эти выражения x-1;y+2;z-2 соответственно равны -7;-1;-3. Тогда

x-1=-7⇔x=-6

y+2=-1⇔y=-3

z-2=-3⇔z=-1. Следовательно координаты точки D(-6,-3,-1)

Так как диагональ точкой пересечения делится пополам, то точка пересечения диагоналей это середина диагонали, диагональ - отрезок соединяющий 2 несоседние вершины, значит найдем середину BD или АС

Координаты середины отрезка находятся по формуле среднего арифмитеческого соответствующих координат концов, т.е. абсцисса первой точки+ абсцисса второй точки делить на 2, ордината и апликата соответственно, тогда

Середина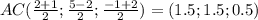 $AC(\frac{2+1}{2};\frac{5-2}{2};\frac{-1+2}{2})=(1.5;1.5;0.5)$ Точка с этими координатами,пусть точка О, и есть точка пересечения диагоналей.

Длина AB .длина вектора это есть квадратный корень из суммы квадратов его координат, тогда длина АВ = длине вектора АВ

|(в)АВ|=

$|AB|=\sqrt{(-7)^2+(-1)^2+(-3)^2}=\sqrt{49+1+9}=\sqrt{59}$

0,0(0 оценок)

Ответ:

Nikol56

29.04.2022 06:07

Пирамида правильная, значит в основании квадрат и боковые ребра равны между собой и равны L. Высота проецируется в центр основания - точку пересечения диагоналей квадрата - О.

SO - высота пирамиды, ∠CSD = α - плоский угол при вершине.

Если конус вписан в пирамиду, то его высота совпадает с высотой пирамиды, а основание - круг, вписанный в основание пирамиды.

ΔCSD: по теореме косинусов

CD² = CS² + DS² - 2CS·DS·cosα = L² + L² - 2·L·L·cosα = 2L²·(1 - cosα)

CD = L√(2(1 - cosα))

Радиус круга, вписанного в квадрат, равен половине стороны квадрата:

r = CD/2 = L√(2(1 - cosα)) / 2 - радиус основания конуса.

CO = AC/2 = CD√2/2 = 2L√(1 - cosα)/4 = L√(1 - cosα)

Из треугольника COS по теореме Пифагора

SO = √(SC² - OC²) = √(L² - L²(1 - cosα)) = L√cosα

Vц = 1/3 · πr² · SO = 1/3 · π ·L²(2(1 - cosα))/4 · L√cosα = πL³ (1 - cosα)√cosα/6

Воспользуемся формулой синуса половинного угла: 2sin²(α/2) = 1 - cosα: