Від точки а відкладено вектор ав=а знайдіть координати точки B ,якщо A(2 7 0) B(-2 -5 0)

Показать ответ

Ответ:

ZorinaMasha2512

09.08.2021 14:51

V = 6224,272 * √3 π см³

Объяснение:

Рассмотрим осевое сечение конуса (см. рис.). SO — высота конуса (h), AO — радиус (r), AS — образующая конуса (43,8 см). Тогда по теореме Пифагора r² + h² = 43,8².

Объём конуса вычисляется по формуле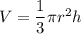 $V=\dfrac{1}{3}\pi r^2h$ . Из предыдущего уравнения r² = 43,8² - h². Подставим это в уравнение объёма:

$V=\dfrac{1}{3}\pi (43{,}8^2-h^2)h=\dfrac{43{,}8^2\pi}{3}h-\dfrac{\pi}{3}h^3$

Найдём максимальное значение с производной:

$V'(h)=\dfrac{43{,}8^2\pi}{3}-\pi h^2\\V'(h)=0\Leftrightarrow \dfrac{43{,}8^2\pi}{3}=\pi h^2\Leftrightarrow h=\pm\dfrac{43{,}8}{\sqrt{3}}$

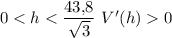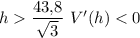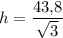Будем рассматривать только положительные значения h, так как отрицательной высота быть не может. При , при $h\dfrac{43{,}8}{\sqrt{3}}\ V'(h)$ . Значит, $h=\dfrac{43{,}8}{\sqrt{3}}$ — точка максимума. При данном значении h объём конуса максимален.

$V_{\max}=\dfrac{1}{3}\pi\left(43{,}8^2-\dfrac{43{,}8^2}{3}\right)\cdot\dfrac{43{,}8}{\sqrt{3}}=\dfrac{1}{3}\pi \cdot\dfrac{2}{3}\cdot 43{,}8\cdot 43{,}8\cdot\dfrac{43{,}8}{3}\sqrt{3}=\\=14{,}6\cdot 2\cdot 14{,}6\cdot 14{,}6\sqrt{3}\pi=6224{,}272\sqrt{3}\pi$

Задача с конусом!! Вычислить наибольший объём конуса, если длина образующей равна 43,8 см: V = [проп

0,0(0 оценок)

Ответ:

zlata25148

15.08.2021 15:44

Объяснение:

1. АН - перпендикуляр к плоскости из точки А.

2. АВ - наклонная к плоскости из точки А.

3. ВН - проекция наклонной на плоскость альфа.

4. Н - основание перпендикуляра АН (или точка пересечения плоскости прямой АН)

5.В - основание наклонной (или точка пересечения плоскости прямой АВ)

6. Расстоянием от точки до плоскости является длина перпендикуляра опущенного из этой точки до плоскости. Следовательно АН = 5 см и есть искомое расстояние.

7. АВН - пифагоров треугольник и катет ВН = 12 см. Но если хочется посчитать, то Пифагор в

BH^2 = AB^2 - A^2 = 13^2 - 5^2 = 169 - 25 = 144/

Тогда ВН = 12 см

0,0(0 оценок)

Популярные вопросы: Геометрия