Катет (меньший) -напротив угла в 30, он равен половине гипотенузы, то есть 1 часть +2 части=3 части
42:3=14 см-меньший катет
14*2=28 см-гипотенуза
3 задача
Строим острый угол В. Из вершины угла проводим окружность, радиусом равным длине гипотенузы. Так как треугольник — прямоугольный, то из точки пересечения окружности и угла С, опускаем перпендикуляр на противоположную сторону. В месте
пересечения перпендикуляра и стороны угла будет точка А. Попарно соединяем вершины треугольника. Искомый треугольник построен*. фото к 3 задаче
1 задача расстояние от т О до MN назовем OQ
рассм. тр-к MOK и MOQ
- угол QMO = углу KOM (MS бисс)
- MO общая
- угол Q = угол K
тр-ки равны ⇒ OQ = OK = 9 см
Объяснение:
2 задача
A=60, <B=30, <C=90
Катет (меньший) -напротив угла в 30, он равен половине гипотенузы, то есть 1 часть +2 части=3 части
42:3=14 см-меньший катет
14*2=28 см-гипотенуза
3 задача
Строим острый угол В. Из вершины угла проводим окружность, радиусом равным длине гипотенузы. Так как треугольник — прямоугольный, то из точки пересечения окружности и угла С, опускаем перпендикуляр на противоположную сторону. В месте
пересечения перпендикуляра и стороны угла будет точка А. Попарно соединяем вершины треугольника. Искомый треугольник построен*. фото к 3 задаче
Дано:
ΔABC, ∠B = 90°.
Вписанная окружность с центром O и радиусом OD = OE = OF,
D∈BC, E∈AC, F∈AB.
OE = 12 (см), EC = 8 (см).
Найти:
Заметим, что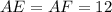 и
и  (так как отрезки касательных, проведенных к окружности из одной точки, равны).
(так как отрезки касательных, проведенных к окружности из одной точки, равны).
Пусть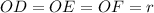 .
.
Тогда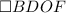 - квадрат, так как
- квадрат, так как  (и, значит,
(и, значит, 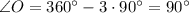 ), а также
), а также 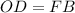 ,
,  и
и 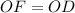 . - Все стороны и углы данного четырехугольника равны.
. - Все стороны и углы данного четырехугольника равны.
Значит,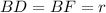 .
.
Тогда катеты треугольника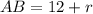 и
и 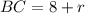 , а гипотенуза равна
, а гипотенуза равна 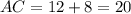 .
.
По тереме Пифагора:
Второй корень нам не подходит (он отрицательный ... ).
Так что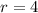 .
.
Можем найти площадь:
Задача решена!
96 см².