Объяснение:
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
1) прямая DC1 и плоскость A1B1C1
DD1 ⊥ (A1B1C1) ⇒ DD1 ⊥ D1C1 ⇒ D1C1 - проекция прямой DC1 на плоскость A1B1C1, а ∠DС1D1 - искомый угол.
Рассмотрим ΔDС1D1 (∠D1=90°):
D1C=A1B1=AB=5
DD1=AA1=12
tg ∠DС1D1 = D1D1/C1D1 = 12/5
∠DС1D1 = arctg (12/5)
2) прямая B1D и плоскость ABC
BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD ⇒ BD - проекция прямой B1D на плоскость ABC, а ∠B1DB- искомый угол.
Рассмотрим ΔB1DB (∠B=90°):
BB1=AA1=12
BD найдём из прямоугольного ΔABD(∠A=90°) по т.Пифагора:
BD² =AB²+AD²=25+49=74
tg ∠B1DB=BB1/BD= = =
∠B1DB= arctg
Рассмотрим прямоугольный △ABC:
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠А = 90° - 45° = 45°.
Т.к. ∠А = ∠В = 45°, то △ABC - равнобедренный.
Т.к. CD Ʇ AB ⇒ CD - высота, проведённая к основанию равнобедренного тр-ка.
Высота, проведённая к основанию равнобедренного треугольника, является и медианой, и высотой.
⇒ высота CD - медиана равнобедренного △ABC.
Медиана, проведённая из прямого угла прямоугольного треугольника к гипотенузе, равна половине гипотенузы.
⇒ медиана CD в 2 раза меньше AB, т.е. AB = 14 (см).
Рассмотрим прямоугольный △PKF:
∠1 + ∠KPC = 180˚, т.к. они смежные ⇒ ∠KPC = 180˚ - 150˚ = 30˚.
Катет, лежащий напротив угла в 30°, равен половине гипотенузы.
⇒ катет KE в 2 раза меньше РЕ, т.е. РЕ = 20 (см).
⇒ ∠PKC = 90˚ - 30˚ = 60˚.
Т.к. ∠PKC = 60˚, а ∠PKE = 90˚ ⇒ ∠CKE = 90˚ - 60˚ = 30˚.
⇒ катет CE в 2 раза меньше KE, т.е. CE = 5 (см).
Т.к. PE = 20 (см), а СЕ = 5 (см), то СР = 20 - 5 = 15 (см).
Пусть отрезок, делящий △ABC на два других будет называться BD.
1. Рассмотрим прямоугольный △DBC:
⇒ ∠DBC = 90˚ - 65˚ = 25˚.
2. Рассмотрим прямоугольный △ABC:
Т.к. на рисунке ∠ABD = ∠DBC, то BD - биссектриса ∠ABC ⇒ ∠ABC = 50˚.
⇒ ∠CAB = 90˚ - 50˚ = 30˚.
Объяснение:
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
1) прямая DC1 и плоскость A1B1C1
DD1 ⊥ (A1B1C1) ⇒ DD1 ⊥ D1C1 ⇒ D1C1 - проекция прямой DC1 на плоскость A1B1C1, а ∠DС1D1 - искомый угол.
Рассмотрим ΔDС1D1 (∠D1=90°):
D1C=A1B1=AB=5
DD1=AA1=12
tg ∠DС1D1 = D1D1/C1D1 = 12/5
∠DС1D1 = arctg (12/5)
2) прямая B1D и плоскость ABC
BB1 ⊥ (ABC) ⇒ BB1 ⊥ BD ⇒ BD - проекция прямой B1D на плоскость ABC, а ∠B1DB- искомый угол.
Рассмотрим ΔB1DB (∠B=90°):
BB1=AA1=12
BD найдём из прямоугольного ΔABD(∠A=90°) по т.Пифагора:
BD² =AB²+AD²=25+49=74
tg ∠B1DB=BB1/BD=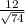 =
=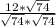 =
= 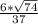
∠B1DB= arctg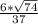
Рассмотрим прямоугольный △ABC:
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠А = 90° - 45° = 45°.
Т.к. ∠А = ∠В = 45°, то △ABC - равнобедренный.
Т.к. CD Ʇ AB ⇒ CD - высота, проведённая к основанию равнобедренного тр-ка.
Высота, проведённая к основанию равнобедренного треугольника, является и медианой, и высотой.
⇒ высота CD - медиана равнобедренного △ABC.
Медиана, проведённая из прямого угла прямоугольного треугольника к гипотенузе, равна половине гипотенузы.
⇒ медиана CD в 2 раза меньше AB, т.е. AB = 14 (см).
ответ: АВ = 14 (см).Задача #2.Рассмотрим прямоугольный △PKF:
∠1 + ∠KPC = 180˚, т.к. они смежные ⇒ ∠KPC = 180˚ - 150˚ = 30˚.
Катет, лежащий напротив угла в 30°, равен половине гипотенузы.
⇒ катет KE в 2 раза меньше РЕ, т.е. РЕ = 20 (см).
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠PKC = 90˚ - 30˚ = 60˚.
Т.к. ∠PKC = 60˚, а ∠PKE = 90˚ ⇒ ∠CKE = 90˚ - 60˚ = 30˚.
Катет, лежащий напротив угла в 30°, равен половине гипотенузы.
⇒ катет CE в 2 раза меньше KE, т.е. CE = 5 (см).
Т.к. PE = 20 (см), а СЕ = 5 (см), то СР = 20 - 5 = 15 (см).
ответ: CE = 5 (см); CP = 15 (см).Задача #3.Пусть отрезок, делящий △ABC на два других будет называться BD.
1. Рассмотрим прямоугольный △DBC:
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠DBC = 90˚ - 65˚ = 25˚.
2. Рассмотрим прямоугольный △ABC:
Т.к. на рисунке ∠ABD = ∠DBC, то BD - биссектриса ∠ABC ⇒ ∠ABC = 50˚.
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠CAB = 90˚ - 50˚ = 30˚.
ответ: ∠CAB = 30˚.