Опусти перпендикуляр из вершины С на АД: СМ ⊥ АД .
Тогда ВСМН - прямоугольник , противоположные стороны которого равны, ВС=МН и ВН=СМ , но так как по условию ВС=ВН, то ВСМН - квадрат, сторону которого обозначим "а" .
ΔАВН - прямоугольный, с углом ∠А=45° . Тогда и ∠АВН=90°-45°=45° .
ответ: h=5 см .
АВСД - трапеция, АВ=СД , ∠А=∠Д=45° ,
ВС=а , ВН ⊥ АД , h=ВН=ВС=а , S(трап)=50см² .
Опусти перпендикуляр из вершины С на АД: СМ ⊥ АД .
Тогда ВСМН - прямоугольник , противоположные стороны которого равны, ВС=МН и ВН=СМ , но так как по условию ВС=ВН, то ВСМН - квадрат, сторону которого обозначим "а" .
ΔАВН - прямоугольный, с углом ∠А=45° . Тогда и ∠АВН=90°-45°=45° .
То есть ΔАВН - равнобедренный и АН=ВН=а .
Аналогично, из ΔСДМ получаем, что ДМ=СМ=а .
Тогда АД=АН+НМ+МД=а+а+а=3а .
Площадь трапеции :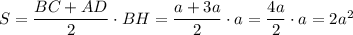
По условию: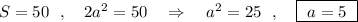
Условие задачи составлено не корректно:
Объяснение:
Решение 1) ( Не используем параметр <ВСD=60°)
∆АСD- прямоугольный треугольник
По теореме Пифагора
СD=√(AC²-AD²)=√(18²-13²)=√(324-169)=
=√155см
P(ABCD)=2(AD+CD)=2(13+√155)=
=26+2√155см
ответ: 26+2√155см
Решение 2) (Не используем теорему Пифагора)
∆АСD- прямоугольный треугольник
<СDA=90°; <ACD=60°; <CAD=30°
СD- катет против угла 30°
СD=AC/2=18/2=9см.
Р=2(АD+DC)=2(13+9)=2*22=44см
Решение 3)
(Не используем параметр диагональ АС)
<САD=30°
tg<CAD=CD/AD
tg30°=1/√3
1/√3=CD/13
CD=13/√3=13√3/3 см
Р=2(13+13√3/3)=2(39/3+13√3/3)=(2(39+13√3))/3=(78+26√3)/3 см.
Решение 4)
(Параметр АD≠13;)
СD=AC/2=9 см катет против угла 30°
cos<CAD=AD/AC
cos30°=√3/2
√3/2=AD/18
AD=18√3/2=9√3см
Р=2(АD+CD)=2(9+9√3)=18+18√3см
ответ: 18+18√3
Zmeura1204