Үшбұрыштың теңдік белгілері. 1. Егер бірінші үшбұрыштың екі қабырғасы мен олардың арасындағы бұрышы екінші үшбұрыштың сәйкес екі қабырғасы мен арасындағы бұрышқа тең болса, онда бұл үшбұрыштар тең болады. 2. Егер бірінші үшбұрыштың бір қабырғасы және оған іргелес жатқан екі бұрышы екінші үшбұрыштың сәйкес қабырғасы мен оған іргелес жатқан екі бұрышына тең болса, онда бұл үшбұрыштар тең болады. 3. Егер бір үшбұрыштың үш қабырғасы екінші үшбұрыштың сәйкес үш қабырғасына тең болса, онда бұл үшбұрыштар тең болады.
Обозначим центр малой окружности через . Если окружность касается хорды, то по свойствам касательной радиус окружности перпендикулярен хорде в этой точке: .
Если отрезок перпендикулярен хорде, то при их пересечении он делит хорду пополам (это теорема, которую изучают в школе). Значит, точка — середина хорды . Треугольник равнобедренный (поскольку отрезки и равны как радиусы). Значит, медиана является также и высотой. Получим, что . Учитывая предыдущее равенство, получим, что . Это значит, что точки и лежат на одной прямой. Тогда на той же прямой лежит точка касания (ведь по условию она диаметрально противополож
Үшбұрыштың теңдік белгілері. 1. Егер бірінші үшбұрыштың екі қабырғасы мен олардың арасындағы бұрышы екінші үшбұрыштың сәйкес екі қабырғасы мен арасындағы бұрышқа тең болса, онда бұл үшбұрыштар тең болады. 2. Егер бірінші үшбұрыштың бір қабырғасы және оған іргелес жатқан екі бұрышы екінші үшбұрыштың сәйкес қабырғасы мен оған іргелес жатқан екі бұрышына тең болса, онда бұл үшбұрыштар тең болады. 3. Егер бір үшбұрыштың үш қабырғасы екінші үшбұрыштың сәйкес үш қабырғасына тең болса, онда бұл үшбұрыштар тең болады.
См. рисунок.
Обозначим центр малой окружности через
. Если окружность касается хорды, то по свойствам касательной радиус окружности перпендикулярен хорде в этой точке: 
.
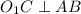Если отрезок перпендикулярен хорде, то при их пересечении он делит хорду пополам (это теорема, которую изучают в школе). Значит, точка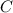
— середина хорды 
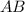. Треугольник 
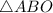равнобедренный (поскольку отрезк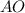и 
и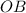 
равны как радиусы). Значит, медиана 
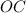является также и высотой. Получим, что 
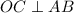. Учитывая предыдущее равенство, получим, что 
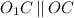. Это значит, что точки 
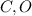и 
лежат на одной прямой. Тогда на той же прямой лежит точка касания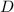 
(ведь по условию она диаметрально противополож