В окружности с центром в точке О к хорде KD, равной
радиусу окружности, перпендикулярно проведен диаметр FE. Диаметр
FE и хорда KD пересекаются в точке А. Длина отрезка KА равна 9,6 см.
a) постройте рисунок по условию задачи;
b) определите длину хорды KD;
c) определите длину диаметра FE;
d) найдите периметр треугольника ОKD.

Показать ответ

Ответ:

JeepandChira13

20.07.2021 20:20

Объяснение:

При длине рейки в 3 см достичь точки (4,5) невозможно, поскольку расстояние от начала первой рейки до конца второй (в случае, если обе рейки лежат на одной прямой) составляет 3 + 3 = 6 см, а кратчайшее расстояние до точки (4,5) составляет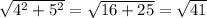 $\sqrt{4^2+5^2}=\sqrt{16+25}=\sqrt{41}$ , что больше 6.

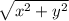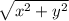Допустим, нужная нам точка имеет координаты (x,y), а длина рейки равна S. Тогда кратчайшее расстояние до точки равно $\sqrt{x^2+y^2}$ , и 2 рейки в сочетании с этим расстоянием составляют равнобедренный треугольник со сторонами S, S и $\sqrt{x^2+y^2}$ .

По теореме косинусов в треугольнике со сторонами a, b и c и углом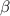 $\beta$ справедливо соотношение 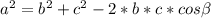$a^2=b^2+c^2-2*b*c*cos\beta$ . Для нашего треугольника данное выражение примет вид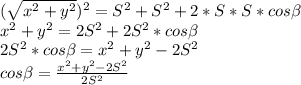 $(\sqrt{x^2+y^2})^2=S^2+S^2+2*S*S*cos\beta\\x^2+y^2=2S^2+2S^2*cos\beta\\2S^2*cos\beta=x^2+y^2-2S^2\\cos\beta=\frac{x^2+y^2-2S^2}{2S^2}$

Отсюда искомый угол будет равен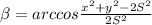 $\beta=arccos\frac{x^2+y^2-2S^2}{2S^2}$ .

0,0(0 оценок)

Ответ:

макс10710

27.10.2022 04:41

1) 31,5

2) 42

Объяснение:

1)Чтобы найти площадь используя катеты, есть специальная формула. S=(a*b) :2. Теперь умножаем катеты и делим их на два. То есть 7*9=63:2=31,5

ответ: 31,5

2)В равнобедренном треугольнике медиана является одновременно и высотой. Поэтому получается 2 прямоугольных треугольника. Основание делится на пополам из за медианы. Поэтому 12:2=6см, это первый катет. А медиана является вторым катетом. Теперь опять же используем формулу площади которую я писала сверху. S=7*6=42:2=21. То что мы получили 21, это площадь одного треугольника. А мы в начале делили этот треугольник на два. Поэтому 21+21=42

ответ :42

0,0(0 оценок)

Популярные вопросы: Геометрия