1)пусть M - точка пересечения медиан треугольника ABC, тогда M - центр треугольника ABC, следовательно, точка М равноудалена от вершин треугольника => перпендикуляр, восстановленный к плоскости треугольника ABC из точки М проходит через точку S.( М - проекция точки S на плоскость ABC). 2) рассмотрим плоскость треугольника АВС. АМ - часть медианы от вершины А до точки пересечения медиан, тогда, согласно теореме о пересечении медиан, АМ=2/3*AA1, где AA1 - медиана из точки А. Рассмотрим треугольник АА1В. Он прямоугольный с острым углом 60 градусов, следовательно АА1 равна 3*sin60, 3*sqrt(3)/2, тогда АМ равна sqrt(3). 3) Рассмотрим треугольник AMS, где MS - расстояние от точки S до плоскости(длина перпендикуляра), а AS - искомое расстояние. Тогда, согласно теореме Пифагора, AS=sqrt(121+3)=sqrt(124)=2*sqrt(31). ответ:2*sqrt(31).
2) рассмотрим плоскость треугольника АВС. АМ - часть медианы от вершины А до точки пересечения медиан, тогда, согласно теореме о пересечении медиан, АМ=2/3*AA1, где AA1 - медиана из точки А. Рассмотрим треугольник АА1В. Он прямоугольный с острым углом 60 градусов, следовательно АА1 равна 3*sin60, 3*sqrt(3)/2, тогда АМ равна sqrt(3).
3) Рассмотрим треугольник AMS, где MS - расстояние от точки S до плоскости(длина перпендикуляра), а AS - искомое расстояние. Тогда, согласно теореме Пифагора, AS=sqrt(121+3)=sqrt(124)=2*sqrt(31).
ответ:2*sqrt(31).
Объяснение:
Дано: SABCD - правильная четырехугольная пирамида.
Боковые грани – правильные треугольники.
ABCD - квадрат.
SO = 4√2 см.
Найти: S полн.
По условию все ребра пирамиды равны.
1. Рассмотрим ΔACD - прямоугольный.
Пусть AD = DC = а
По теореме Пифагора:
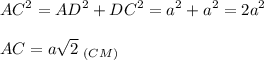
Диагонали квадрата точкой пересечения делятся пополам.⇒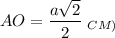
2. Рассмотрим ΔAOS - прямоугольный.
По теореме Пифагора:
3. S полн. = S осн. +S бок.
S бок. равна площади четырех равносторонних треугольников.
Площадь равностороннего треугольника найдем по формуле:
⇒ S бок. = 32√3 * 4 = 128√3 (см²)
Площадь основания:
Площадь полной поверхности:
S полн. = (128√3 + 64) см²