В основании пирамиды - ромб со сторонами 8 см и углом 30 градусов. боковые грани пирамиды образуют с плоскостью основания углы 60 градусов. Найдите площадь поверхности пирамиды.
1. Апофема L определяется по т Пифагора L²=h²+(a/2)²=100+4=104, L = = 2 ≈ 10,2 см
Объяснение:
2. Площадь основания находится как площадь равностороннего Δ с со стороной a, So = a²/4=4. Аопофема L находится из условия L²=b²-(a/2)²=64-2,25=61,75, L ≈ 7,59 cм, тогда площадь 1 Грани = aL/2 ≈ 1,5·7,59≈11,78 cм², а вся площадь боковой поверхности = утроенной площади боковой грани ≈ 33,36 см². Общая площадь = 4√3+33,36 ≈33,36+6,93 ≈ 40,29 ≈ 40 см²
3. Диагональ основания d =6, тогда высота находится из соотношения h² = b²-(d/2)²=144-18=126, h =3, площадь основания So=a²=36, объём V=Soh/3=36≈ 95,25 ≈ 95 см²
1. Апофема L определяется по т Пифагора L²=h²+(a/2)²=100+4=104, L =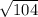
= 2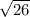
≈ 10,2 см
Объяснение:
2. Площадь основания находится как площадь равностороннего Δ с со стороной a, So =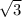
a²/4=4
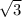. Аопофема L находится из условия L²=b²-(a/2)²=64-2,25=61,75, L ≈ 7,59 cм, тогда площадь 1 Грани = aL/2 ≈ 1,5·7,59≈11,78 cм², а вся площадь боковой поверхности = утроенной площади боковой грани ≈ 33,36 см². Общая площадь = 4√3+33,36 ≈33,36+6,93 ≈ 40,29 ≈ 40 см²
3. Диагональ основания d =6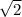
, тогда высота находится из соотношения h² = b²-(d/2)²=144-18=126, h =3
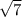, площадь основания So=a²=36, объём V=Soh/3=36
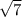≈ 95,25 ≈ 95 см²
a ∩ b.
Один из углов в 4 раза > другого.
Найти :Больший угол = ?
Решение :При пересечении двух прямых образуются четыре угла.
∠1 = ∠3, ∠2 = ∠4 (это пары вертикальных углов. Они равны между собой по свойству вертикальных углов).
Пусть ∠2 = х.
Тогда, по условию задачи, один из углов должен быть равен 4х.
Естественно, что ∠4 ≠ 4х, так как уже ∠4 = х по выше сказанному.
Тогда пусть ∠1 = 4х.
∠1 и ∠2 - смежные (по определению).
Сумма смежных углов равна 180°.Отсюда :
∠1 + ∠2 = 180°
4х + х = 180°
5х = 180° ⇒ х = 180° : 5 = 36°
4х = 4*36° = 144°.
(Естественно, что за 4х мы брали самый больший угол, поэтому в ответ пойдёт значение 4х).
ответ :144°.