В параллелограмме АВСD основание ВC равно 10. Точка Р не лежит в плоскости параллелограмма, точка К - середина отрезка ВР. Плоскость ADK пересекает отрезок РС в точке М. Найдите длину отрезка К М. Найдите длину отрезка К м.

Показать ответ

Ответ:

оопгп

13.01.2022 15:23

АС=√7см

Объяснение:

Дано:

ABCD- трапеция

АВ=CD=√3см

BC=1см

<ABC=150°

АС=?

___________

В равнобокой трапеции углы при основаниях равны.

<АВС=<ВСD

<BAD=<CDA

В трапеции сумма углов прилежащих к боковой стороне равна 180°

<СDA=180°-<BCD=180°-150°=130°

Проведём две высоты СК и ВМ.

АМ=KD

∆CKD- прямоугольный.

sin<CDK=CK/CD

sin30°=1/2

1/2=CK/√3

CK=√3/2 см.

cos<CDK=KD/CD

cos30°=√3/2

√3/2=KD/√3

KD=√3√3/2=1,5см.

ВС=МК=1см

АК=АМ+МК=1,5+1=2,5см

∆АСК- прямоугольный треугольник

По теореме Пифагора

АС²=АК²+СК²=2,5²+(√3/2)²=6,25+0,75=7см

АС=√7см

В равнобедренной трапеции меньшее основание ровно 1 см боковая сторона равна корень 3 а большой угол

0,0(0 оценок)

Ответ:

Bayana000

09.10.2022 18:12

$\boxed{FK = 5}$

Объяснение:

Дано: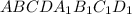 $ABCDA_{1}B_{1}C_{1}D_{1}$ - правильная усеченная четырехугольная пирамида, 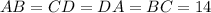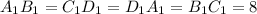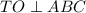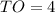AB = CD = DA = BC = 14 , $A_{1}B_{1} = C_{1}D_{1} = D_{1}A_{1} = B_{1}C_{1} = 8$ , $TO \perp ABC$ , TO = 4 , AK = KB,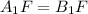 $A_{1}F = B_{1}F$

Найти: FK - ?

Решение: По свойствам правильной усеченной четырехугольной пирамиды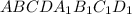 $ABCDA_{1}B_{1}C_{1}D_{1}$ её основаниями являются квадраты, а высота пирамиды проходит через центры квадратов. Так точка O - точка пересечения диагоналей квадрата ABCD, то диагонали точкой пересечения делятся пополам по свойствам квадрата. Так как диагонали квадрата равны по теореме, то и половины диагоналей также равны, тогда AO = OB и треугольник ΔAOB - равнобедренный. Так как для треугольника ΔAOB отрезок OK - медиана

(по условию AK = KB), то по теореме медиана равнобедренного треугольника проведенная к основания является биссектрисой и высотой. Треугольник ΔBOK подобен треугольнику ΔBDA по двум углам так как угол ∠OBK - общий и OK ⊥ AB, и DA ⊥ AB.

Так как ΔBOK подобен треугольнику ΔBDA:

$\dfrac{OK}{DA} = \dfrac{BK}{BA} \Longrightarrow OK = \dfrac{DA \cdot BK}{AB} = \dfrac{DA \cdot BK}{2BK} = \dfrac{AD}{2} = \dfrac{14}{2} = 7$ .

Так как квадрат ABCD подобен квадрату $A_{1}B_{1}C_{1}D_{1}$ так как все углы квадрата равны 90°, то можно записать отношения соответствующих элементов квадрата:

$\dfrac{FT}{KO} = \dfrac{A_{1}B_{1}}{AB} \Longrightarrow FT = \dfrac{KO\cdot A_{1}B_{1}}{AB} = \dfrac{7 * 8}{14} = \dfrac{56}{14} = 4$ .

TFOK - трапеция так как FT║OK по свойствам правильной усеченной четырехугольной пирамиды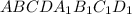 $ABCDA_{1}B_{1}C_{1}D_{1}$ . Рассмотрим трапеция TFOK.Трапеция TFOK - прямоугольная так как по условию 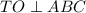$TO \perp ABC$ и OK ⊂ ABC .Проведем высоту из точки F в точку H на основании OK. Так как FH - высота трапеции и TO - высота трапеции, то FH = TO = 4. По свойствам трапеции четырехугольник TOHF - прямоугольник, тогда его противоположные стороны равны по свойствам прямоугольника и TF = OH = 4. OK = OH + HK ⇒ HK = OK - OH = 7 - 4 = 3. Рассмотрим прямоугольный (FH ⊥ OK по построению) треугольник ΔFHK. 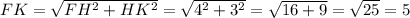По теореме Пифагора: $FK = \sqrt{FH^{2} + HK^{2}} = \sqrt{4^{2} + 3^{2}}= \sqrt{16 + 9 }= \sqrt{25} = 5$ .