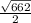В правильной четырехугольной пирамиде боковое ребро длиной 18 см наклонено к плоскости основания под углом 45градусов. Найти площадь полной поверхности и объем пирамиды.
Как известно, центр тяжести треугольника это точка пересечение его медиан.
Медианы треугольника пересекаются в одной точке и в точке пересечения делятся в отношении 1:2
При повороте треугольника на 180 градусов вокруг центра тяжести, каждая сторона нового треугольника параллельна соответствующей стороне исходного и пересекает часть медианы между ее вершиной и центром тяжести пополам.
Из этого следует что от исходного треугольника этой стороной отсекается "маленький" треугольник подобный исходному но все размеры которого в три раза меньше. Следовательно его площадь в 9 раз меньше площади исходного.
Таких "маленьких" треугольников три и они не входят в общую часть треугольников после поворота. Следовательно общая часть имеет площадь равную площади исходного S минус три площади "маленьких" треугольников 3 * S/9
Имеем S - 3*S/9 = S - S/3 = S *2/3
Таким образом площадь общей части составляет 2/3 от площади исходного треугольника.
Не выяснили, чем всё-таки являются числа в условии, так что я приму их за длины сторон треугольника АВС, где АВ=27, ВС=22, АС=42.
Здесь пригодится теорема косинусов: , где угол альфа - угол напротив стороны а.
Применим теорему для стороны АВ: АВ²=ВС²+АС²-2ВС*АС*cosBCA
27²=22²+42²-2*22*42*cosBCA
729=484+1764-1848cosBCA
1848cosBCA=1519
cosBCA=
Аналогично применяем теорему для оставшихся углов и получаем:
cosСАВ=
cosСВА= -
Чтобы дальше решать было удобнее, обозначим точки пересечения медиан и сторон треугольника: медиана из угла А пересекает сторону СВ в точке К, медиана из угла В пересекает сторону АС в точке L, а медиана из угла С пересекает сторону АВ в точке М. Теперь вычислим длины медиан. Как известно, медианы делят стороны, к которым проведены, пополам. Таким образом получаем: AL=LC=42/2=21, CK=KB=22/2=11, BM=MA=27/2=13,5.
Здесь опять нужна теорема косинусов, только теперь необходимо найти одну из сторон при известном косинусе и двух других сторонах.
2/3
Объяснение:
Как известно, центр тяжести треугольника это точка пересечение его медиан.
Медианы треугольника пересекаются в одной точке и в точке пересечения делятся в отношении 1:2
При повороте треугольника на 180 градусов вокруг центра тяжести, каждая сторона нового треугольника параллельна соответствующей стороне исходного и пересекает часть медианы между ее вершиной и центром тяжести пополам.
Из этого следует что от исходного треугольника этой стороной отсекается "маленький" треугольник подобный исходному но все размеры которого в три раза меньше. Следовательно его площадь в 9 раз меньше площади исходного.
Таких "маленьких" треугольников три и они не входят в общую часть треугольников после поворота. Следовательно общая часть имеет площадь равную площади исходного S минус три площади "маленьких" треугольников 3 * S/9
Имеем S - 3*S/9 = S - S/3 = S *2/3
Таким образом площадь общей части составляет 2/3 от площади исходного треугольника.
а) 217/264, 287/324, -551/1188; б)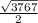
, 
, 
.
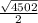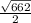Объяснение:
Не выяснили, чем всё-таки являются числа в условии, так что я приму их за длины сторон треугольника АВС, где АВ=27, ВС=22, АС=42.
Здесь пригодится теорема косинусов: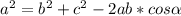
, где угол альфа - угол напротив стороны а.
Применим теорему для стороны АВ: АВ²=ВС²+АС²-2ВС*АС*cosBCA
27²=22²+42²-2*22*42*cosBCA
729=484+1764-1848cosBCA
1848cosBCA=1519
cosBCA=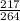
Аналогично применяем теорему для оставшихся углов и получаем:
cosСАВ=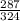
cosСВА= -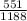
Чтобы дальше решать было удобнее, обозначим точки пересечения медиан и сторон треугольника: медиана из угла А пересекает сторону СВ в точке К, медиана из угла В пересекает сторону АС в точке L, а медиана из угла С пересекает сторону АВ в точке М. Теперь вычислим длины медиан. Как известно, медианы делят стороны, к которым проведены, пополам. Таким образом получаем: AL=LC=42/2=21, CK=KB=22/2=11, BM=MA=27/2=13,5.
Здесь опять нужна теорема косинусов, только теперь необходимо найти одну из сторон при известном косинусе и двух других сторонах.
СМ²=АС²+АМ²-2АМ*АС*cosСАВ
СМ²=42²+13,5²-2*13,5*42*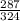
СМ=√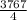
СМ=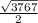
Аналогично поступаем и с другими медианами:
АК=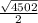
BL=