В правильной четырехугольной призме ABCDA1B1C1D1 точка M принадлежит плоскости BB1K, где K- середина ребра CD. Построить сечение,проходящее через точку M перпендикулярно ребру СС1.

1) 8 2) 8

Объяснение:

Прости, без синусов и косинусов не получится, но вот решение

В треугольнике ABC <А=15, <B=75, значит <С=180-15-75=90

Треугольник ABC - прямоугольный и АВ - гипотенуза

Формула длины высоты через гипотенузу и острые углы:

Н=с*sin α*cos α=AB*sin 15*cos 15

AB=H : sin 15*cos 15=2 : sin 15*cos 15=2 : (1/2*sin 30)=4 : 1/2=8.

А вот тут получется без sin и cos.

Для начала, нужно построить рисунок, после построения мы видим, что DH=2, и он лежит против угла DBH, который равен 30 градусам, значит BH=4. ВН лежит против угла С, который равен 30 градусам, значит ВС равен 8.

ответ: 8

2

Объяснение:

Найдем сначала x. Пусть окружность касается AB и BC в точках K и L соответственно. Тогда BK=BL=x. Аналогично CL=x. Тогда BC=2x => x=1. Радиус, проведенный в точку касания, перпендикулярен к касательной. Тогда, если O - центр окружности, OK=OL=R и OK⊥AB, а OL⊥BC. Значит ∠KBL+∠KOL=180°. Тогда по теореме косинусов для четырехугольника KBLO можно выразить KL² двумя через OK=OL=R и BK=BL=1. Приравняем KL². Получим: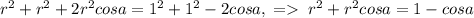 . Здесь cosa - косинус ∠KBL. 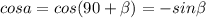, где 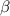- угол ABH. AB=10x=10, а AH=(14-2)/2=6 => 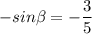. Подставим это: .

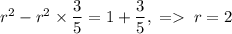Задание выполнено!