В прямом параллелепипеде боковое ребро равно 12 см, большая сторона основания 7 см, большая диагональ основания 9 см. Найдите площадь боковой поверхности параллелепипеда, если его большая диагональ образует с большей стороной основания угол с решением и рисунком.
а) (-2;0) - центр окружности, радиус окружности равен 3.
б) (0; 4) - центр окружности, радиус окружности равен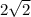 .
.
в) (5; -7) - центр окружности, радиус окружности равен 4.
Объяснение:
Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.
а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.
б) (0; 4) - центр окружности,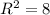 ,
, 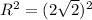
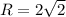 .
.
в) (5; -7) - центр окружности, R²=16,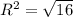 , R=4.
, R=4.
Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень
а) (-2;0) - центр окружности, радиус окружности равен 3.
б) (0; 4) - центр окружности, радиус окружности равен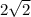 .
.
в) (5; -7) - центр окружности, радиус окружности равен 4.
Объяснение:
Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.
а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.
б) (0; 4) - центр окружности,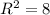 ,
, 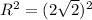
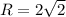 .
.
в) (5; -7) - центр окружности, R²=16,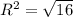 , R=4.
, R=4.
Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень