В прямоугольном треугольнике ABC из прямого угла C провели высоту CN, которая разбивает гипотенузу на два отрезка длиной 9 см и 25 см. Найдите длину высоты CN.
Примечание: решите задачу, учитывая, что высота прямоугольного треугольника разбивает его на два треугольника, подобных исходному.
CN=15
Объяснение:
AN=9
BN=25
CN=?
Высота CN, есть среднее пропорциональное между проекциями катетов на гипотенузу=>
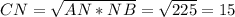
Проведем высоту CN.
ABC и ACN прямоугольные и имеют общий угол A, следовательно они подобны по двум углам.
Аналогично ABC и CBN прямоугольные и имеют общий угол B, следовательно подобны.
Треугольники ACN и CBN оба подобны ABC, следовательно подобны друг другу. Их соответствующие стороны пропорциональны.
ACN~CBN => AN/CN=CN/BN => CN^2 =AN*BN
Доказали, что высота из прямого угла равна среднему пропорциональному проекций катетов.
CN =√(25*9) =15 (см)