В прямоугольном треугольнике угол между высотой и медианой, проведёнными из вершины прямого угла, равен 67°. Найди больший из острых углов этого треугольника ABC. ответ дай в градусах.
1.два кути називаються суміжними, якщо в них одна сторона спільна а дві інші є доповняльними променями 2сума суміжних кутив дорівнюе 180 градусів 3 два кути називаються вертикальними якщо сторони одного кута є доповняльними променями сторин другого якщо вертикальні кути є розгорнутими то вони рівно 4 перпендикулярними 5 дві прямі називаються паралельними якщо вони не перетинаються 6 дві перпендикулярними якщо при їхньому перетині утворивня прямий кут 7 що не перетинаються 8відрізок 9кут який мае вершіну кута та три сторони
№1. Проведем AD — перпендикуляр к плоскости α. АВ и АС — проекции наклонных DB и DC на плоскость α. Треугольники DAB и DAC — прямоугольные. Так что DC = а : sin45° = a√2 ; DB = а : sin30° = 2a.
Далее, ΔBDC — прямоугольный (по условию). Тогда по теореме Пифагора: BC = = = =
№2. Пусть D - данная точка. DB и DC - наклонные. Проведем AD — перпендикуляр к плоскости α. Тогда АВ и АС — проекции наклонных на плоскость α. Тогда ΔABD и ΔACD — прямоугольные, равнобедренные. Так что АВ = АC = AD = а.
DC = DB = a : sin45 =
Так что ΔBDC — равнобедренный, а поскольку ∠BDC = 60°, то значит треугольник BDC — равносторонний, т.е.
2сума суміжних кутив дорівнюе 180 градусів
3 два кути називаються вертикальними якщо сторони одного кута є доповняльними променями сторин другого
якщо вертикальні кути є розгорнутими то вони рівно
4 перпендикулярними
5 дві прямі називаються паралельними якщо вони не перетинаються
6 дві перпендикулярними якщо при їхньому перетині утворивня прямий кут
7 що не перетинаються
8відрізок
9кут який мае вершіну кута та три сторони
Вариант 1
№1. Проведем AD — перпендикуляр к плоскости α. АВ и АС — проекции наклонных DB и DC на плоскость α. Треугольники DAB и DAC — прямоугольные. Так что DC = а : sin45° = a√2 ; DB = а : sin30° = 2a.
Далее, ΔBDC — прямоугольный (по условию). Тогда по теореме Пифагора: BC =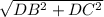 =
= 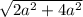 =
= 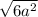 =
= 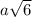
№2. Пусть D - данная точка. DB и DC - наклонные. Проведем AD — перпендикуляр к плоскости α. Тогда АВ и АС — проекции наклонных на плоскость α. Тогда ΔABD и ΔACD — прямоугольные, равнобедренные. Так что АВ = АC = AD = а.
DC = DB = a : sin45 =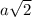
Так что ΔBDC — равнобедренный, а поскольку ∠BDC = 60°, то значит треугольник BDC — равносторонний, т.е.
DB = DC = BC =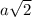
(Дальше долко)