В прямоугольный треугольник с углом 60 вписана окружность радиуса 4. Найти его стороны. В р/б трапецию с углом 60 вписана окружность радиуса 7. Найти площадь.
т.к треугольник равнобедренный, то высота это и медиана и биссектриса. следовательно получим два равных прямоугольных треугольника. углы в них 90 30 и 60 градусов
(углы при основании большого треугольника равны так как это равнобедренный треугольник и равны соответственно 180 - 120=60\2=30)
свойство прямоугольных треугольников, что катет лежащий против угла в 30 градусов равен половине гипотенузы
следовательно гипотенуза равна 23*2=46 см
по теореме пифагора находим основание маленького треугольника это 46^=23^2 +x^2
случае наименьший угол равен ∠ =
180
Объяснение:Рассмотрим треугольник ABC с углами ∠ = ∠ = , ∠ = 180 − 2. Чтобы
получилось два треугольника прямая должна проходить через одну из вершин.
Рассмотрим случай, когда она проходит через вершину A и делит треугольник на два: ADB
и ADC (см. рис.).
Треугольник ADC является равнобедренным в двух случаях:
I) ∠ = . Приравнивая ∠ = ∠ (т.к. угол ∠ тупой) приходим к
уравнению 180 − 2 = 3 − 180
, откуда = 72
. Наименьший угол тогда
равен ∠ = 36
II) ∠ = ∠ =
180−
2
. Тогда 3
2
− 90 = 180 − 2, откуда =
540
7
т.к треугольник равнобедренный, то высота это и медиана и биссектриса. следовательно получим два равных прямоугольных треугольника. углы в них 90 30 и 60 градусов
(углы при основании большого треугольника равны так как это равнобедренный треугольник и равны соответственно 180 - 120=60\2=30)
свойство прямоугольных треугольников, что катет лежащий против угла в 30 градусов равен половине гипотенузы
следовательно гипотенуза равна 23*2=46 см
по теореме пифагора находим основание маленького треугольника это 46^=23^2 +x^2
х= 23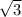
основание большого треугольника 23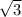 *2 = 46
*2 = 46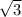
Объяснение: